【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
参考答案:
【答案】C
【解析】由题中条件可得△ACD≌△BDC,再利用边角关系得△AOD≌△BOC,△ABD≌△BAC,进而可得出结论.
∵∠1=∠2,∠3=∠4,又CD为公共边,所以△ACD≌△BDC(AAS),故A正确,不符合题意;
∵△ACD≌△BDC,∴AC=BD,AD=BC,又∵AB=BA,∴△ABD≌△BAC(SSS),故B正确,不符合题意;
∵△ACD≌△BDC,∴AC=BD,∵∠3=∠4,∴OC=OD,∴OA=OB,
又∵∠AOD=∠GOC,∴△AOD≌△BOC(SAS),故D正确,不符合题意;
由已知无法说明C选项正确,故C符合题意,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
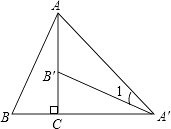
A.70°
B.65°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=
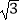 ,则弧BN的长为 .
,则弧BN的长为 . 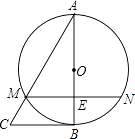
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD为高线,若AB+BD=CD,AC=4
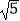 ,BD=3,则线段BC的长度为 .
,BD=3,则线段BC的长度为 . -
科目: 来源: 题型:
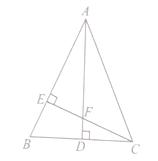
查看答案和解析>>【题目】如图,在△ABC中,AB=AC, AD是∠BAC的平分线,AD⊥BC, CE⊥AB.CE交AD于点F,AE=CE.
(1)你能说明△AEF与△CEB全等吗?
(2)若AF=12cm,求CD的长.
相关试题

