【题目】在△ABC中,AD为高线,若AB+BD=CD,AC=4 ![]() ,BD=3,则线段BC的长度为 .
,BD=3,则线段BC的长度为 .
参考答案:
【答案】5或11
【解析】解:如图1中,设AB=x,则CD=AB+BD=3+x, 
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2﹣BD2=AC2﹣CD2 ,
∴x2﹣32=(4 ![]() )2﹣(x+3)2 ,
)2﹣(x+3)2 ,
解得x=5或﹣8(舍弃),
∴BC=BD+CD=3+3+5=11.
如图2中,设AB=x,则CD=AB+BD=3+x,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2﹣BD2=AC2﹣CD2 ,
∴x2﹣32=(4 ![]() )2﹣(x+3)2 ,
)2﹣(x+3)2 ,
解得x=5或﹣8(舍弃),
∴BC=CD﹣BD=5,
所以答案是5或11.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
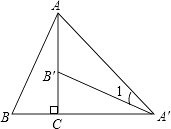
A.70°
B.65°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=
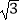 ,则弧BN的长为 .
,则弧BN的长为 . 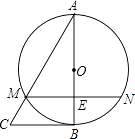
-
科目: 来源: 题型:
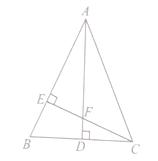
查看答案和解析>>【题目】如图,在△ABC中,AB=AC, AD是∠BAC的平分线,AD⊥BC, CE⊥AB.CE交AD于点F,AE=CE.
(1)你能说明△AEF与△CEB全等吗?
(2)若AF=12cm,求CD的长.
-
科目: 来源: 题型:
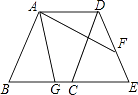
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×8的网格中,每个小正方形的边长均为1,线段AB的顶点均在小正方形的顶点上.
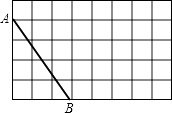
(1)画出等腰直角△ABC,点C在格点上;
(2)画出有一个锐角的正切值是2的直角△ABD,点D在格点上;
(3)在(1)(2)的条件下,连接CD,请直接写出△BCD的面积.
相关试题

