【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )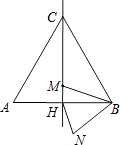
A.![]() a
a
B.a
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:如图,取BC的中点G,连接MG,
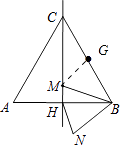
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB= ![]() AB,
AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,
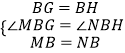 ,
,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,MG⊥CH时,MG最短,即HN最短,
此时∵∠BCH= ![]() ×60°=30°,CG=
×60°=30°,CG= ![]() AB=
AB= ![]() ×2a=a,
×2a=a,
∴MG= ![]() CG=
CG= ![]() ×a=
×a= ![]() ,
,
∴HN= ![]() ,
,
所以答案是:D.
【考点精析】通过灵活运用等边三角形的性质和含30度角的直角三角形,掌握等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°。
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由)

-
科目: 来源: 题型:
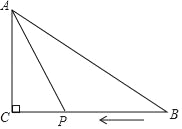
查看答案和解析>>【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
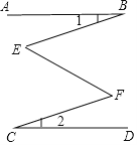
【答案】相等,理由见解析.
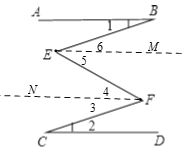
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.
【题型】解答题
【结束】
26【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为
 ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离; 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为 ,目标C的位置表示为
,目标C的位置表示为 .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )
A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
相关试题

