【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
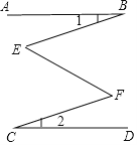
【答案】相等,理由见解析.
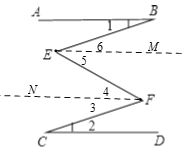
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.
【题型】解答题
【结束】
26
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
参考答案:
【答案】(1)0,1,2;(2)证明见解析;(3)![]()
【解析】试题分析:(1)根据0次幂的意义和乘方的意义进行计算即可;
(2)观察各等式得到2的相邻两个非负整数幂的差等于其中较小的2的非负整数幂,即2n-2n-1=2n-1(n为正整数);
(3)由于21-20=20,22-21=21,23-22=22,…22018-22017=22017,然后把等式左边与左边相加,右边与右边相加即可求解.
试题解析:(1)21-20=1=20;22-21=2=21;23-22=4=22,
故答案为:0,1,2;
(2)观察可得:2n-2n-1=2n-1(n为正整数),证明如下:
2n-2n-1=2×2n-1-2n-1=2n-1×(2-1)=2n-1;
(3)∵21-20=20,
22-21=21,
23-22=22,
…
22018-22017=22017,
∴22018-20=20+21+22+23+…+22016+22017,
∴20+21+22+23+…+22016+22017的值为22018-1.
-
科目: 来源: 题型:
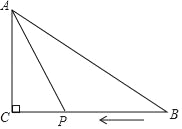
查看答案和解析>>【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
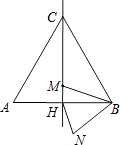
A.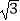 a
a
B.a
C.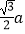
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为
 ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离; 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为 ,目标C的位置表示为
,目标C的位置表示为 .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )
A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
-
科目: 来源: 题型:
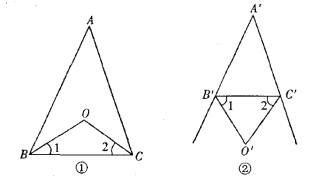
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;
(3)上面(1)(2)两题中的∠BOC与∠B′O′C′ 有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′ 是否还具有这样的关系?这个结论你是怎样得到的?
-
科目: 来源: 题型:
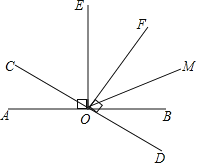
查看答案和解析>>【题目】如图,已知直线AB与CD相交于点0,OE⊥AB,OF⊥CD,OM是∠BOF的角平分线
(1)若∠AOC=25°,求∠BOD和∠COE的度数.
(2)若∠AOC=a,求∠EOM的度数(用含a的代数式表示)
相关试题

