【题目】如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°。
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由)

参考答案:
【答案】(1)10°;(2)![]() .
.
【解析】
(1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠DAE,然后求解即可;
(2)分两种情况,利用(1)中的数据关系直接得出答案即可.
解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
∵AE是角平分线,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() ×100°=50°,
×100°=50°,
∵AD是高,
∴∠BAD=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
(2)当∠C>∠B时,如图1,
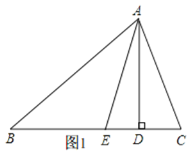
根据三角形的内角和得,∠BAC=180°-(∠B+∠C),
∵AD是角平分线,
∴∠BAD=![]() ∠BAC=90°-
∠BAC=90°-![]() [180°-(∠B+∠C)]=
[180°-(∠B+∠C)]= ![]() (∠B+∠C)-90°,
(∠B+∠C)-90°,
∵AE是△ABC的高,
∴∠BAE=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-∠B-[![]() (∠B+∠C)-90°]=
(∠B+∠C)-90°]= ![]() (∠C-∠B),
(∠C-∠B),
∴∠DAE=![]() (∠C-∠B).
(∠C-∠B).
当∠C<∠B时,如图2,
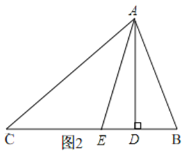
同∠B>∠C的方法得出,∠DAE=![]() (∠B-∠C).
(∠B-∠C).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
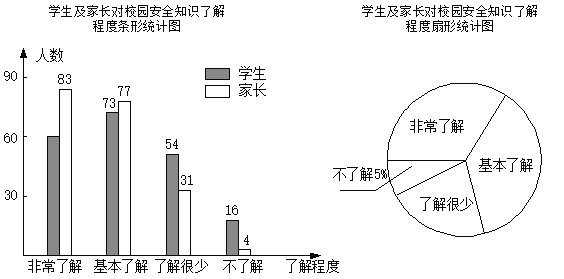
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格中,每个小方格都是边长为1个单位长度的正方形,
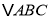 的三个顶点都在格点(小方格的顶点)上.
的三个顶点都在格点(小方格的顶点)上.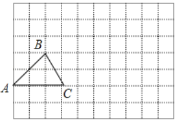
(1)请建立适当的平面直角坐标系,使
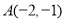 ,
,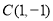 ,并写出点
,并写出点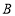 的坐标;
的坐标;(2)在(1)的条件下,将
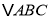 先向右平移4个单位长度再向上平移2个单位长度后可得到
先向右平移4个单位长度再向上平移2个单位长度后可得到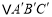 ,请在图中画出平移后的
,请在图中画出平移后的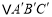 ,并分别写出点
,并分别写出点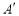 ,
, ,
, 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
-
科目: 来源: 题型:
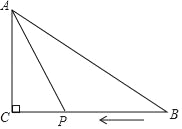
查看答案和解析>>【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
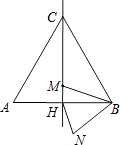
A.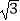 a
a
B.a
C.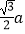
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

相关试题

