【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
参考答案:
【答案】(1)25元;(2) 购进A种跳绳40根,B种跳绳60根时,最大利润为460元.
【解析】试题分析:(1)设A种跳绳的单价为x元,B种跳绳的单价为y元,根据购进A种跳绳10根和B种跳绳7根,共需395元,购进A种跳绳5根和B种跳绳3根,共需185元,列方程组进行求解即可得;
(2)设购进A种跳绳a根,则B种跳绳(100-a)根,该商店的利润为w元,用含a的代数式表示出w,再求出a的取什范围,然后利用一次函数的性质进行求解即可得.
试题解析:(1)设A种跳绳的单价为x元,B种跳绳的单价为y元,
根据题意,得![]() ,解得
,解得![]() ,
,
答:A种跳绳的单价为22元,B种跳绳的单价为25元;
(2)设购进A种跳绳a根,则B种跳绳(100-a)根,该商店的利润为w元,
则w=(26-22)a+(30-25)(100-a)=-a+500,
∵-1< 0 ,∴a取最小值时,w取最大值,
又∵a ≥100×![]() =40,且a为整数,
=40,且a为整数,
∴当a =40时,w最大=-40+500=460(元),
此时,100-40=60,
所以该商店购进A种跳绳40根,B种跳绳60根时可获得最大利润,最大利润为460元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,(1)abc>0;(2)4a+2b+c>0;(3)4ac﹣b2<16a;(4)
 <a<
<a< ;(5)b<c,其中正确的结论有( )
;(5)b<c,其中正确的结论有( )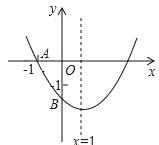
A. (2)(3)(4)(5) B. (1)(3)(4)(5) C. (1)(3)(4) D. (1)(2)(5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成
 ,定义
,定义 =ad-bc,上述记号就叫做2阶行列式.若
=ad-bc,上述记号就叫做2阶行列式.若 =-20,求x的值.
=-20,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为
 (分),且
(分),且 (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:组别
成绩
 (分)
(分)频数(人数)
频率
一

2

二

10
0.2
三

12

四


0.4
五

6


请根据表格提供的信息,解答以下问题:
(1)本次决赛共有__________名学生参加;
(2)直接写出表中:
 ___________
___________ ____________
____________(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2
 ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )

A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.

相关试题

