[题目]在课题学习中.老师要求用长为12厘米.宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角.然后沿虚线折成一个无盖的长方体纸盒．甲:如图1.盒子底面的四边形ABCD是正方形,乙:如图2.盒子底面的四边形ABCD是正方形,丙:如图3.盒子底面的四边形ABCD是长方形.AB=2AD．将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列.正确的是A.甲题目和参考答案 ——青夏教育精英家教网—

【题目】在课题学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒．

甲：如图1，盒子底面的四边形ABCD是正方形；

乙：如图2，盒子底面的四边形ABCD是正方形；

丙：如图3，盒子底面的四边形ABCD是长方形，AB=2AD．

将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列，正确的是

A.甲＞乙＞丙B.甲＞丙＞乙C.丙＞甲＞乙D.丙＞乙＞甲

参考答案：

【答案】C

【解析】

分别将甲乙丙三位同学折成的无盖长方体的容积计算出来，即可比较大小.

甲：长方体的长为5cm，宽为3 cm，高为3 cm，容积为

乙：长方体的长为10 cm，宽为2 cm，高为2 cm，容积为

丙：长方体的长为6 cm，宽为4 cm，高为2 cm，容积为

所以，丙＞甲＞乙

故选C

相关试题

科目： 来源： 题型：

【题目】若 x 满足 (9x)(x4)=4，求 (4x)2+(x9)2 的值.
设 9x=a，x4=b，则 (9x)(x4)=ab=4，a+b=(9x)+(x4)=5 ，
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题：
(1)若 x 满足 (5x)(x2)=2，求 (5x)2+(x2)2 的值
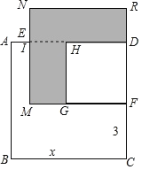
(2)已知正方形 ABCD 的边长为 x ， E ， F 分别是 AD 、 DC 上的点，且 AE=1 ， CF=3 ，长方形 EMFD 的面积是 48 ，分别以 MF 、 DF 作正方形，求阴影部分的面积.
查看答案和解析>>
科目： 来源： 题型：

【题目】现在正是草莓热销的季节，某水果零售商店分两批次从批发市场共购进草莓40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
（1）设第一、二次购进草莓的箱数分别为a箱、b箱，求a，b的值；
（2）若商店对这40箱草莓先按每箱60元销售了x箱，其余的按每箱35元全部售完．
①求商店销售完全部草莓所获利润y（元）与x（箱）之间的函数关系式；
②当x的值至少为多少时，商店才不会亏本．（注：按整箱出售，利润＝销售总收入－进货总成本）
查看答案和解析>>
科目： 来源： 题型：

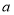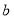
【题目】如图1，长方形纸片ABCD的两条边AB、BC的长度分别为、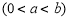，小明它沿对角线AC剪开，得到两张三角形纸片（如图2），再将这两张三角纸片摆成如图3的形状，点A、B、D、E在同一条直线上，且点B与点D重合，点B、F、C也在同一条直线上．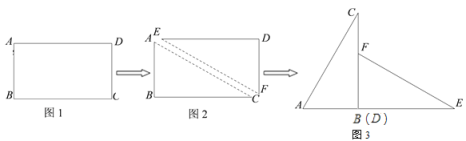
（1）将图3中的△ABC沿射线AE方向平移，使点B与点E重合，点A、C分别对应点M、N，按要求画出图形，并直接写出平移的距离；（用含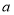或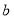的代数式表示）
（2）将图3中的△DEF绕点B逆时针方向旋转60°，点E、F分别对应点P、Q，按要求画出图形，并直接写出∠ABQ的度数；
（3）将图3中的△ABC沿BC所在直线翻折，点A落在点G处，按要求画出图形，并直接写出GE的长度．（用含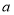、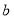的代数式表示）
查看答案和解析>>
科目： 来源： 题型：

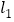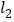【题目】如图，∥，BE∥CF，BA⊥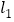，DC⊥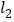，下面给出四个结论：①BE＝CF；②AB＝DC；③；
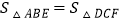④四边形ABCD是矩形．其中说法正确的有（）
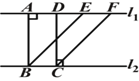
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目： 来源： 题型：

【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号，立即出发，沿北偏东67°方向航行10海里到达小岛C处，将人员撤离到位于码头A正东方向的码头B，测得小岛C位于码头B的北偏西53°方向，求码头A与码头B的距离．【参考数据：sin23°≈0.39，cos23°≈0.92，tan23°≈0.42，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75】
查看答案和解析>>
科目： 来源： 题型：

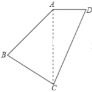
【题目】如图，在四边形ABCD中，AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，则∠DAB的度数是______°．
查看答案和解析>>