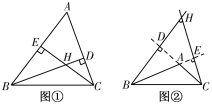
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H.找出∠BHC和∠A之间存在何种等量关系;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
参考答案:
【答案】 (1)∠A+∠BHC=180° (2)仍然成立
【解析】
(1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;
(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.
(1)由∠BHC与∠EHD是对顶角,得:
∠BHC=∠EHD,
由高BD、CE相交于点H,得:
∠ADH=∠AEH=90°,
由四边形内角和定理,得:
∠A+∠AEH+∠EHD+∠HDA=360°,
∠A+∠EHD=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠A=180°;
(2)由∠BHC与∠EHD是对顶角,得:
∠BHC=∠EHD,
由高BD、CE相交于点H,得:
∠ADH=∠AEH=90°,
由四边形内角和定理,得:
∠H+∠AEH+∠EHD+∠HDA=360°,
∠H+∠DAE=360°-∠AEH-∠HDA=360°-90°-90°=180°,
∴∠BHC+∠BAC=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直径为10cm的⊙O中,弦AB的长为5
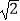 cm,则AB所对的圆周角是 .
cm,则AB所对的圆周角是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】探究活动有一圆柱形食品盒,它的高等于8cm,底面直径为
 cm,蚂蚁爬行的速度为2cm/s
cm,蚂蚁爬行的速度为2cm/s(1)如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)

(2)如果在盒外下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
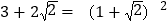 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
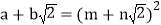 (其中
(其中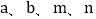 均为整数),则有
均为整数),则有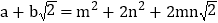 .
.∴
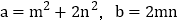 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分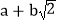 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
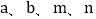 均为正整数时,若
均为正整数时,若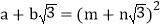 ,用含m、n的式子分别表示
,用含m、n的式子分别表示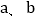 ,得
,得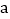 = ,
= ,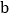 = ;
= ;(2)利用所探索的结论,找一组正整数
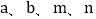 ,填空: + =( +
,填空: + =( + 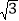 )2;
)2;(3)若
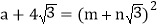 ,且
,且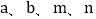 均为正整数,求
均为正整数,求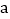 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
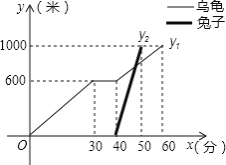
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法共有____________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
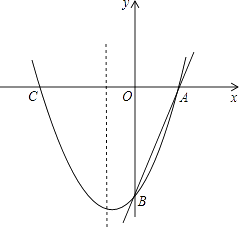
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
相关试题

