【题目】已知:一次函数 ![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点 ![]() ,
,![]() .
.
(1)分别求出这两个函数的表达式;
(2)直接写出当一次函数的函数值大于反比例函数的函数值时,![]() 的取值范围为______.
的取值范围为______.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或 ![]()
【解析】
(1)先利用待定系数法确定反比例函数解析式,再确定Q点坐标,然后再利用待定系数法确定一次函数解析式;
(2)观察两函数图象得到当x<-3或0<x<2时,一次函数图象都在反比例函数图象上方.
(1)由题意得:
将 ![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
![]() 反比例函数的解析式为
反比例函数的解析式为![]() ;
;
将 ![]() 代入
代入 ![]() ,得
,得 ![]() ,
,
![]() .
.
将 ![]() ,
,![]() 代入
代入 ![]() ,得
,得 ![]()
![]()
![]() 一次函数的解析式为
一次函数的解析式为![]() .
.
(2)当x<-3或0<x<2时,一次函数的函数值大于反比例函数的函数值.
故答案为x<-3或0<x<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.

(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:给定两个不等式组
 和
和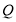 ,若不等式组
,若不等式组 的任意一个解,都是不等式组
的任意一个解,都是不等式组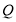 的一个解,则称不等式组
的一个解,则称不等式组 为不等式组
为不等式组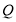 的“子集”。例如:不等式组:
的“子集”。例如:不等式组: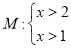 是:
是: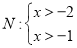 的“子集”。
的“子集”。(1)若不等式组:
 ,
,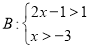 ,则其中不等式组 是不等式组
,则其中不等式组 是不等式组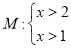 的“子集”(填
的“子集”(填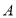 或
或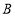 );
);(2)若关于
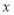 的不等式组
的不等式组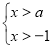 是不等式组
是不等式组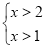 的“子集”,则
的“子集”,则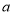 的取值范围是 ;
的取值范围是 ;(3)已知
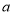 ,
,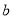 ,
,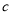 ,
,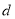 为互不相等的整数,其中
为互不相等的整数,其中 ,
,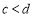 ,下列三个不等式组:
,下列三个不等式组: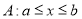 ,
,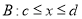 ,
, 满足:
满足: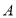 是
是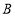 的“子集”且
的“子集”且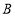 是
是 的“子集”,求
的“子集”,求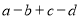 的值;
的值;(4)已知不等式组
 有解,且是不等式组
有解,且是不等式组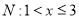 的“子集”,则满足条件的有序整数对
的“子集”,则满足条件的有序整数对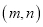 共有多少个?
共有多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5
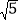 米,tanB=
米,tanB= ,∠C=30°.
,∠C=30°.(1)求桥面AD与地面BC之间的距离.
(2)因受地形限制,决定对该天桥进行改建,使CD斜面的坡度变陡,将其30°坡角改为40°,改建后斜面为DG,试计算此次改建节省路面宽度CG大约应是多少?(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,
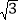 ≈1.732)
≈1.732)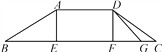
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
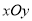 中,
中,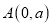 ,
,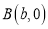 分别在
分别在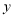 轴正半轴和
轴正半轴和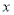 轴负半轴上,
轴负半轴上,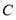 在第二象限,满足:
在第二象限,满足: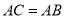 ,
,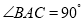 .已知
.已知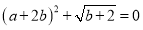 .
.(1)求
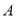 ,
,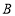 的坐标;
的坐标;(2)求点
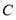 的坐标及
的坐标及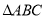 的面积;
的面积;(3)已知
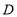 是
是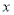 轴的正半轴上一点,
轴的正半轴上一点,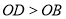 ,
,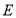 在第一象限,
在第一象限,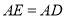 ,
,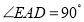 ,连接
,连接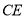 交
交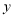 轴于点
轴于点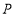 .
.①求证:
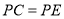 .
.②在点
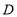 的移动过程中,给出以下两个结论:(i)
的移动过程中,给出以下两个结论:(i)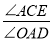 的值不变;(ii)
的值不变;(ii)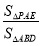 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值. 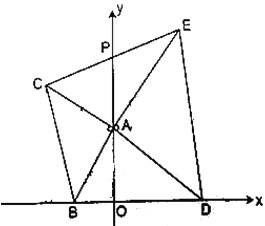
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
相关试题

