【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.

(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
参考答案:
【答案】(1)见解析;(2)AE=BD,AE⊥BD,理由见解析;(3)△AED的面积为![]() .
.
【解析】
(1)由已知条件可推导得到![]() ,由SAS即可证明△ABE≌△BCD;
,由SAS即可证明△ABE≌△BCD;
(2)由(1)可得△ABE≌△BCD 可得AE=BD,再由角的转化可得∠AFB=90°,即可证明AE⊥BD;
(3)因为 △AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可求解△AED的面积.
(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中, ,
,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=![]() (1+2)×2﹣
(1+2)×2﹣![]() ×2×1﹣
×2×1﹣![]() ×1×1=
×1×1=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】第一届中非经贸博览会于
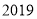 年
年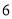 月
月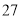 日至
日至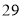 日在长沙举办,为了抓住商机,某服装店决定购进甲、乙两种文化衫进行销售,若购进甲种文化衫
日在长沙举办,为了抓住商机,某服装店决定购进甲、乙两种文化衫进行销售,若购进甲种文化衫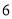 件,乙种文化衫
件,乙种文化衫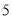 件,需要
件,需要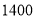 元;若购进甲种文化衫
元;若购进甲种文化衫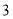 件,乙种文化衫
件,乙种文化衫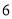 件,需要
件,需要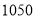 元.
元.(1)求购进甲、乙两种文化衫每件各需多少元?
(2)若该服装店决定用不超过
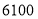 元的资金购进这两种服装共
元的资金购进这两种服装共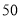 件,且用于购买甲种文化衫的资金不低于购买乙种文化衫的资金,那么该商店共有哪几种进货方案?
件,且用于购买甲种文化衫的资金不低于购买乙种文化衫的资金,那么该商店共有哪几种进货方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:给定两个不等式组
 和
和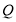 ,若不等式组
,若不等式组 的任意一个解,都是不等式组
的任意一个解,都是不等式组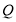 的一个解,则称不等式组
的一个解,则称不等式组 为不等式组
为不等式组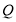 的“子集”。例如:不等式组:
的“子集”。例如:不等式组: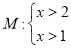 是:
是: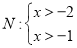 的“子集”。
的“子集”。(1)若不等式组:
 ,
,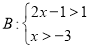 ,则其中不等式组 是不等式组
,则其中不等式组 是不等式组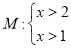 的“子集”(填
的“子集”(填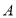 或
或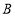 );
);(2)若关于
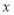 的不等式组
的不等式组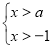 是不等式组
是不等式组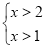 的“子集”,则
的“子集”,则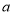 的取值范围是 ;
的取值范围是 ;(3)已知
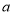 ,
,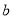 ,
,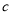 ,
,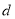 为互不相等的整数,其中
为互不相等的整数,其中 ,
,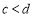 ,下列三个不等式组:
,下列三个不等式组: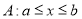 ,
,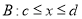 ,
, 满足:
满足: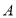 是
是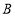 的“子集”且
的“子集”且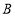 是
是 的“子集”,求
的“子集”,求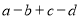 的值;
的值;(4)已知不等式组
 有解,且是不等式组
有解,且是不等式组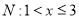 的“子集”,则满足条件的有序整数对
的“子集”,则满足条件的有序整数对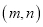 共有多少个?
共有多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数
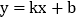 的图象与反比例函数
的图象与反比例函数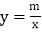 的图象交于点
的图象交于点 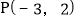 ,
, .
.(1)分别求出这两个函数的表达式;
(2)直接写出当一次函数的函数值大于反比例函数的函数值时,
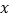 的取值范围为______.
的取值范围为______.
相关试题

