搜索
【题目】某日通过高速公路收费站的汽车中，共有3000辆次缴了通行费，其中大车每辆次缴费20元，小车每辆次缴费10元．设这一天小车缴通行费的辆次为x，总的通行费收入为y元。
（1）试写出y关于x的函数关系式，y是x的一次函数吗？是正比例函数吗？
（2）若小车缴通行费的辆次为1000，这天的通行费收入是多少元？
参考答案：
【答案】（1）
，y是x的一次函数，但不是正比例函数；（2）这一天通行费收入为50000元.
【解析】
（1）小车有x辆，则大车有（3000-x）辆，根据：总通行费=小车通行费+大车通行费，列出函数关系式；
（2）把x=1000代入（1）中的函数关系式即可．
解：（1）
y是x的一次函数，但不是正比例函数；
（2）当
时，
（元）．
答：当小车缴通行费的辆次为1000时，这一天通行费收入为50000元.
故答案为：（1），y是x的一次函数，但不是正比例函数；（2）这一天通行费收入为50000元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，矩形OABC的顶点O、A、C的坐标分别为O（0，0），A（﹣x，0），C（0，y），且x、y满足
．（1）矩形的顶点B的坐标是 ．
（2）若D是AB中点，沿DO折叠矩形OABC，使A点落在点E处，折痕为DO，连BE并延长BE交y轴于Q点．
①求证：四边形DBOQ是平行四边形．
②求△OEQ面积．
（3）如图2，在（2）的条件下，若R在线段AB上，AR＝4，P是AB左侧一动点，且∠RPA＝135°，求QP的最大值是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB=10°，点P在OB上．以点P为圆心，OP为半径画弧，交OA于点P1（点P1与点O不重合），连接PP1；再以点P1为圆心，OP为半径画弧，交OB于点P2（点P2与点P不重合），连接P1 P2；再以点P2为圆心，OP为半径画弧，交OA于点P3（点P3与点P1不重合），连接P2 P3；……
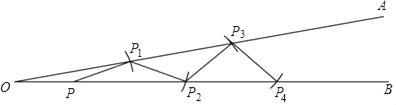
请按照上面的要求继续操作并探究：
∠P3 P2 P4=_____°；按照上面的要求一直画下去，得到点Pn，若之后就不能再画出符合要求点Pn+1了，则n=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某食品厂计划平均每天生产200袋食品，但是由于种种原因，实际每天生产量与计划量相比有出入.下表是某周的生产情况（超过计划量记为正）
（1）根据记录的数据可知该厂星期二生产食品多少袋？
（2）根据记录的数据可知产量最多的一天比产量最少的一天多生产食品多少袋？
（3）根据记录的数据可知该厂本周实际共生产食品多少袋？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知AB∥CD，∠B＝20°，∠D＝110°．
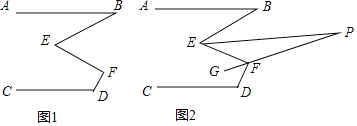
（1）若∠E＝50°，请直接写出∠F的度数；
（2）探索∠E与∠F之间满足的数量关系，并说明理由；
（3）如图2，EP平分∠BEF，FG平分∠EFD，FG的反向延长线交EP于点P，求∠P的度数．
-
科目： 来源： 题型：
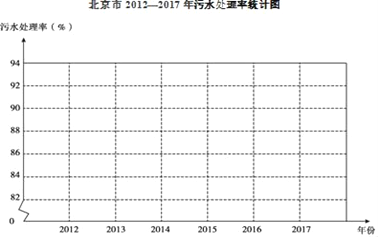
查看答案和解析>>【题目】北京市积极开展城市环境建设，其中污水治理是重点工作之一，以下是北京市2012﹣2017年污水处理率统计表：
年份
2012
2013
2014
2015
2016
2017
污水处理率（%）
83.0
84.6
86.1
87.9
90.0
92.0
（1）用折线图将2012﹣2017年北京市污水处理率表示出来，并在图中标明相应的数据；
（2）根据统计图表中提供的信息，预估2018年北京市污水处理率约为_____%，说明你的预估理由：_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠B＝90°，AB＝BC＝2，AD＝1，CD＝3．
（1）求∠DAB的度数．
（2）求四边形ABCD的面积．
相关试题
