搜索
【题目】如图，矩形OABC中，A（1，0），C（0，2），双曲线y= 
（0＜k＜2）的图象分别交AB，CB于点E，F，连接OE，OF，EF，S△OEF=2S△BEF ， 则k值为（ ）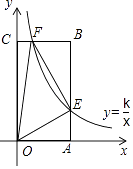
A.
B.1
C.
D.
参考答案：
【答案】A
【解析】解：∵四边形OABC是矩形，BA⊥OA，A（1，0），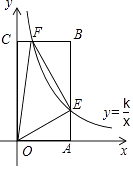 
∴设E点坐标为（1，m），则F点坐标为（ 
，2），
则S△BEF= 
（1﹣ ）（2﹣m），S△OFC=S△OAE= m，
∴S△OEF=S矩形ABCO﹣S△OCF﹣S△OEA﹣S△BEF=2﹣ m﹣ m﹣ （1﹣ ）（2﹣m），
∵S△OEF=2S△BEF，
∴2﹣ m﹣ m﹣ （1﹣ ）（2﹣m）=2 （1﹣ ）（2﹣m），
整理得 
（m﹣2）2+m﹣2=0，解得m1=2（舍去），m2= 
，
∴E点坐标为（1， ）；
∴k= ，
所以答案是：A．
【考点精析】根据题目的已知条件，利用比例系数k的几何意义的相关知识可以得到问题的答案，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“全民阅读”深入人心，好读书，读好书，让人终身受益．为满足同学们的读书需求，学校图书馆准备到新华书店采购文学名著和动漫书两类图书．经了解，20本文学名著和40本动漫书共需1560元，20本文学名著比20本动漫书多360元（注：所采购的文学名著价格都一样，所采购的动漫书价格都一样）．
（1）求每本文学名著和动漫书各多少元？
（2）若学校要求购买动漫书比文学名著多20本，动漫书和文学名著总数不低于74本，总费用不超过2100，请求出所有符合条件的购书方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的半径为5，弦AB长为8，过AB的中点E有一动弦CD（点C只在弦AB所对的劣弧上运动，且不与A、B重合），设CE=x，ED=y，下列图象中能够表示y与x之间函数关系的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，从①∠1＝∠2；②∠C＝∠D；③∠A＝∠F三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为( )
A. 0 B. 1 C. 2 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD的对角线相交于点O，且点O是BD的中点，若AB＝AD＝5，BD＝8，∠ABD＝∠CDB，则四边形ABCD的面积为（ ）
A.40B.24C.20D.15
-
科目： 来源： 题型：
查看答案和解析>>【题目】请把下面证明过程补充完整：
已知：如图，∠ADC＝∠ABC，BE、DF分别平行∠ABC、∠ADC，且∠1＝∠2．
求证：∠A＝∠C．
证明：因为BE、DF分别平分∠ABC、∠ADC，（ ）．
所以∠1＝
∠ABC，∠3＝
∠ADC（ ）．因为∠ABC＝∠ADC（已知），
所以∠1＝∠3（ ），
因为∠1＝∠2（已知），
所以∠2＝∠3（ ）．
所以 ∥ （ ）．
所以∠A＋∠ ＝180°，∠C＋∠ ＝180°（ ）．
所以∠A＝∠C（ ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格；
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；
(3)在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.
相关试题
