【题目】如图,将三角尺的直角顶点放在直线a上,a//b,∠1=50°,∠2=60°,则∠3的度数为( )
A.50°
B.60°
C.70°
D.80°
参考答案:
【答案】C
【解析】先根据三角形内角和定理求出∠4的度数,由对顶角的性质可得出∠5的度数,再由平行线的性质得出结论即可.
∵△BCD中,∠1=50°,∠2=60°,
∴∠4=180°-∠1-∠2=180°-50°-60°=70°,
∴∠5=∠4=70°,
∵a//b,
∴∠3=∠5=70°.
故选C.
【考点精析】本题主要考查了对顶角和邻补角和平行线的性质的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.正数和负数互为相反数
B.-a的相反数是正数
C.任何有理数的绝对值都大于它本身
D.任何一个有理数都有相反数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC于点D.
(1)求证:△BCD为等腰三角形;
(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;
(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.


图1 图2
-
科目: 来源: 题型:
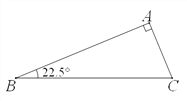
查看答案和解析>>【题目】(1)操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)
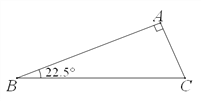
(2)分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;
(3)猜想发现:若一个三角形能被一直线分割成两个等腰三角形,需满足什么条件?(请你至少写出两个条件,无需证明)
-
科目: 来源: 题型:
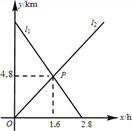
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段
 、
、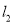 分别表示小敏、小聪离B地的距离
分别表示小敏、小聪离B地的距离 与已用时间
与已用时间 之间的关系,则小敏、小聪行走的速度分别是
之间的关系,则小敏、小聪行走的速度分别是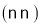
A.
 和
和 B.
B.  和
和
C.
 和
和 D.
D.  和
和
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是直线
 上一定点,点A是x轴上一动点
上一定点,点A是x轴上一动点 不与原点重合
不与原点重合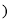 ,连接PA,过点P作
,连接PA,过点P作 ,交y轴于点B,探究线段PA与PB的数量关系.
,交y轴于点B,探究线段PA与PB的数量关系.
 1
1 如图
如图 ,当
,当 轴时,观察图形发现线段PA与PB的数量关系是______;
轴时,观察图形发现线段PA与PB的数量关系是______; 2
2 当PA与x轴不垂直时,在图
当PA与x轴不垂直时,在图 中画出图形,线段PA与PB的数量关系是否与
中画出图形,线段PA与PB的数量关系是否与 Ⅰ
Ⅰ 所得结果相同?写出你的猜想并加以证明;
所得结果相同?写出你的猜想并加以证明; 3
3  为何值时,线段
为何值时,线段 ?此时
?此时 的度数是多少,为什么?
的度数是多少,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为条件,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
条件(已知):
结论(求证):
证明:

相关试题

