【题目】(1)操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)
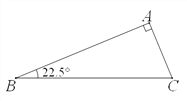
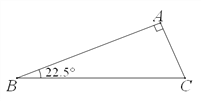
(2)分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;
(3)猜想发现:若一个三角形能被一直线分割成两个等腰三角形,需满足什么条件?(请你至少写出两个条件,无需证明)
参考答案:
【答案】(1)见解析;(2)117°,108°,90°,84°;(3)见解析
【解析】试题分析: ![]() 如图所示,作斜边
如图所示,作斜边![]() 边的中线即可;如图所示,作
边的中线即可;如图所示,作![]() 的平分线即可;
的平分线即可;
![]() 根据等腰三角形的性质进行分割, 写出△ABC最大内角的所有可能值;
根据等腰三角形的性质进行分割, 写出△ABC最大内角的所有可能值;
![]() 根据
根据![]() 直接进行猜想.
直接进行猜想.
试题解析:(1)如图所示:
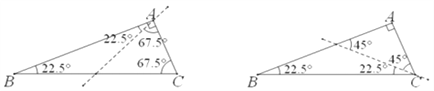
(2)设分割线为AD,相应角度如图所示:
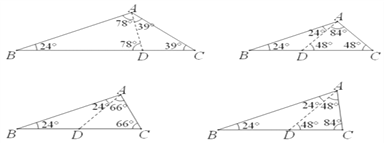
故![]() 的最大内角可能值是
的最大内角可能值是![]()
![]() ①该三角形是一个直角三角形;
①该三角形是一个直角三角形;
②该三角形有一个角是另一个角的2倍;
③该三角形有一个角是另一个角的3倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.正数和负数互为相反数
B.-a的相反数是正数
C.任何有理数的绝对值都大于它本身
D.任何一个有理数都有相反数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC于点D.
(1)求证:△BCD为等腰三角形;
(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;
(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.


图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角尺的直角顶点放在直线a上,a//b,∠1=50°,∠2=60°,则∠3的度数为( )

A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
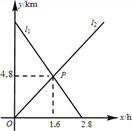
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段
 、
、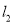 分别表示小敏、小聪离B地的距离
分别表示小敏、小聪离B地的距离 与已用时间
与已用时间 之间的关系,则小敏、小聪行走的速度分别是
之间的关系,则小敏、小聪行走的速度分别是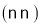
A.
 和
和 B.
B.  和
和
C.
 和
和 D.
D.  和
和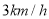
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是直线
 上一定点,点A是x轴上一动点
上一定点,点A是x轴上一动点 不与原点重合
不与原点重合 ,连接PA,过点P作
,连接PA,过点P作 ,交y轴于点B,探究线段PA与PB的数量关系.
,交y轴于点B,探究线段PA与PB的数量关系.
 1
1 如图
如图 ,当
,当 轴时,观察图形发现线段PA与PB的数量关系是______;
轴时,观察图形发现线段PA与PB的数量关系是______; 2
2 当PA与x轴不垂直时,在图
当PA与x轴不垂直时,在图 中画出图形,线段PA与PB的数量关系是否与
中画出图形,线段PA与PB的数量关系是否与 Ⅰ
Ⅰ 所得结果相同?写出你的猜想并加以证明;
所得结果相同?写出你的猜想并加以证明; 3
3  为何值时,线段
为何值时,线段 ?此时
?此时 的度数是多少,为什么?
的度数是多少,为什么?
相关试题

