【题目】(本题10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为条件,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
条件(已知):
结论(求证):
证明:

参考答案:
【答案】条件:①,②;结论:③.证明详见解析.(答案不唯一)
【解析】试题如果①AB⊥BC、CD⊥BC,②BE∥CF作已知条件,那么③∠1=∠2作结论.由垂直的定义可知∠ABC=∠BCD,由平行线的性质可得∠EBC=∠FCB,应用等式的性质即可证得∠1=∠2.
试题解析:条件(已知):①AB⊥BC、CD⊥BC,②BE∥CF,
结论(求证):③∠1=∠2.
证明:因为AB⊥BC、CD⊥BC,所以∠ABC=∠BCD=90°,
因为BE∥CF,所以∠EBC=∠FCB,
因为∠1=∠ABC -∠EBC ,∠2=∠BCD-∠FCB,
所以∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角尺的直角顶点放在直线a上,a//b,∠1=50°,∠2=60°,则∠3的度数为( )

A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段
 、
、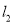 分别表示小敏、小聪离B地的距离
分别表示小敏、小聪离B地的距离 与已用时间
与已用时间 之间的关系,则小敏、小聪行走的速度分别是
之间的关系,则小敏、小聪行走的速度分别是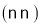
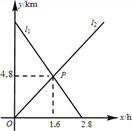
A.
 和
和 B.
B.  和
和
C.
 和
和 D.
D.  和
和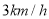
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是直线
 上一定点,点A是x轴上一动点
上一定点,点A是x轴上一动点 不与原点重合
不与原点重合 ,连接PA,过点P作
,连接PA,过点P作 ,交y轴于点B,探究线段PA与PB的数量关系.
,交y轴于点B,探究线段PA与PB的数量关系.
 1
1 如图
如图 ,当
,当 轴时,观察图形发现线段PA与PB的数量关系是______;
轴时,观察图形发现线段PA与PB的数量关系是______; 2
2 当PA与x轴不垂直时,在图
当PA与x轴不垂直时,在图 中画出图形,线段PA与PB的数量关系是否与
中画出图形,线段PA与PB的数量关系是否与 Ⅰ
Ⅰ 所得结果相同?写出你的猜想并加以证明;
所得结果相同?写出你的猜想并加以证明; 3
3  为何值时,线段
为何值时,线段 ?此时
?此时 的度数是多少,为什么?
的度数是多少,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
240
180
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.

A. 1275 B. 2500 C. 1225 D. 1250
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
相关试题

