【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.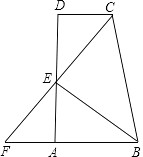
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
参考答案:
【答案】
(1)解:垂直,理由如下:
∵CD∥AB,
∴∠ABC+∠BCD=180°,
又∵∠ABC,∠BCD的角平分线交于E点,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∴∠EBC+∠ECB=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CEB=90°,
∴BE 与 CF 互相垂直.
(2)解:由(1)知∠CEB=90°,
∴∠FEB=90°,
在△FBE 和△CBE 中,
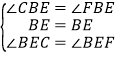
∴△FBE≌△CBE(ASA),
∴BF=BC,EF=EC,
又∵CD∥AB,
∴∠DCE=∠AFE,
在△DCE和△AFE中,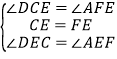
∴△DCE≌△AFE,
∴DC=AF,
∵CD=3,AB=4,
∴BC=BF=AF+AB=CD+AB=3+4=7,
【解析】(1)垂直,理由如下:由两直线平行,同旁内角互补得出∠ABC+∠BCD=180°;又由角平分线定义得出∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
从而得出∠EBC+∠ECB=90°,根据三角形内角和定理得出∠CEB=90°,即BE 与 CF 互相垂直.
(2)由(1)知∠CEB=∠FEB=90°,根据ASA得△FBE≌△CBE,再由全等三角形的性质得出BF=BC,EF=EC;又由两直线平行,内错角相等,得到∠DCE=∠AFE,由ASA得△DCE≌△AFE,再根据全等三角形的性质得出DC=AF,由已知条件和等量代换求出BC的值.
【考点精析】关于本题考查的角的平分线和平行线的性质,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,b)与点Q(2,3)关于x轴对称,则a﹣b=________.
-
科目: 来源: 题型:
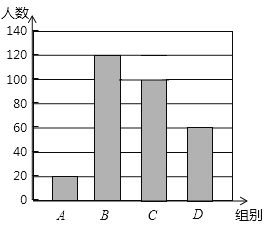
查看答案和解析>>【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )
A. 0.000124 B. 0.0124 C. ﹣0.00124 D. 0.00124
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:
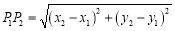 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式: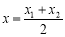 ,
,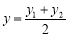 .
.
(1)请你帮小明写出中点坐标公式的证明过程;
运用:(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为 ;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标: ;
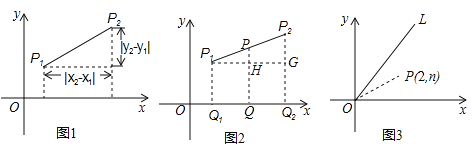
拓展:(3)如图3,点P(2,n)在函数
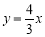 (x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值. -
科目: 来源: 题型:
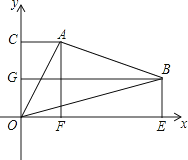
查看答案和解析>>【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程
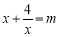 的两实根,且tan∠PCD=
的两实根,且tan∠PCD= ,求⊙O的半径.
,求⊙O的半径.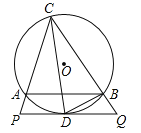
相关试题

