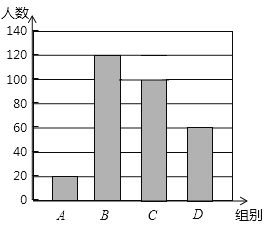
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
参考答案:
【答案】(1)B,C;(2)960.
【解析】
试题分析:(1)根据中位数的概念,中位数应是第150、151人时间的平均数,分析可得答案;
(2)首先计算样本中达到国家规定体育活动时间的频率,再进一步估计总体达到国家规定体育活动时间的人数.
试题解析:(1)众数在B组.
根据中位数的概念,中位数应是第150、151人时间的平均数,分析可得其均在C组,故本次调查数据的中位数落在C组.
故答案为:B,C;
(2)达国家规定体育活动时间的人数约1800×![]() =960(人).
=960(人).
答:达国家规定体育活动时间的人约有960人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.
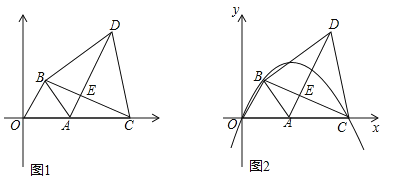
(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数
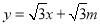 的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P为第三象限的点,P到x轴的距离是2,到y轴的距离是5,那么P点坐标是( )
A. (-2,-5) B. (﹣5,﹣2) C. (﹣5,2) D. (5,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,b)与点Q(2,3)关于x轴对称,则a﹣b=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )
A. 0.000124 B. 0.0124 C. ﹣0.00124 D. 0.00124
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.
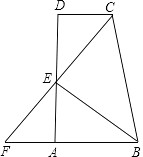
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 . -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:
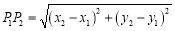 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式: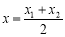 ,
,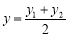 .
.
(1)请你帮小明写出中点坐标公式的证明过程;
运用:(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为 ;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标: ;
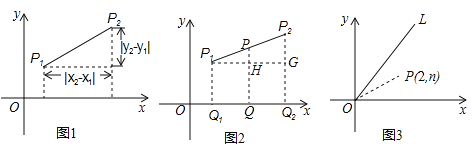
拓展:(3)如图3,点P(2,n)在函数
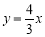 (x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
相关试题

