搜索
【题目】某中学初一年级有350名同学去春游，已知2辆A型车和1辆B型车可以载学生100人，1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人？
(2)若计划租用A型车
辆，租用B型车
辆，请你设计租车方案，能一次运送所有学生，且恰好每辆车都坐满.
参考答案：
【答案】(1)A载30人，B载40人；(2)见解析.
【解析】
（1）设每辆A型车可载学生x人，每辆B型车可载学生y人，根据“2辆A型车和1辆B型车可以载学生100人；1辆A型车和2辆B型车可以载学生110人”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）根据题意可列方程30m+40n=350，由m，n均为正整数，可得所有租车方案.
解：(1)设A、B各载x人、y人；
解得
A型车每辆可载学生30人，B型车每辆可载学生40人；
(2)由题意可知：
30m+40n=350，
符合条件的有：
，
，
三种方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据图形及题意填空，并在括号里写上理由.
己知：如图，
，
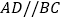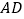平分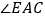
.试说明：
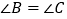.解：因为
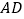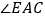平分（已知）所以
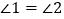（角平分线的定义）因为
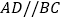（已知）所以∠_________=∠__________（________）
∠____________=∠_________（___________）
所以
.
-
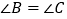科目： 来源： 题型：
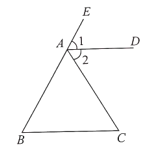
查看答案和解析>>【题目】如图，已知∠1＝∠BDC，∠2＋∠3＝180°．
(1) 请你判断DA与CE的位置关系，并说明理由；
(2) 若DA平分∠BDC，CE⊥AE于点E，∠1＝70°，试求∠FAB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，直线a∥b，直线c与直线a、b分别相交于C、D两点，直线d与直线a、b分别相交于A、B两点，点P在直线AB上运动(不与A、B两点重合)．
(1)如图1，当点P在线段AB上运动时，总有：∠CPD＝∠PCA+∠PDB，请说明理由；
(2)如图2，当点P在线段AB的延长线上运动时，∠CPD、∠PCA、∠PDB之间有怎样的数量关系，并说明理由；
(3)如图3，当点P在线段BA的延长线上运动时，∠CPD、∠PCA、∠PDB之间又有怎样的数量关系(只需直接给出结论)？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AM、BN分别与⊙O相切于点A、B，CD交AM、BN于点D、C，DO平分∠ADC.
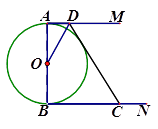
（1）求证：CD是⊙O的切线；
（2）设AD＝4，AB＝x (x > 0)，BC＝y (y > 0). 求y关于x的函数解析式. -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：已知点P（x0 ， y0）和直线y=kx+b，则点P到直线y=kx+b的距离，可用公式d=
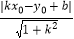计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d= =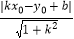 
= 
= 
．
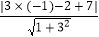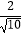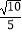根据以上材料，解答下列问题：
（1）求点P（1，﹣1）到直线y=x﹣1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=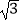
x+9的位置关系并说明理由；
（3）已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上的两点A、B所表示的数分别是a和b,O为数轴上的原点，如果有理数a,b满足
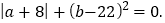
(1)求a和b的值；
(2)若点P是一个动点，以每秒5个单位长度的速度从点A出发，沿数轴向右运动，请问经过多长时间，点P恰巧到达线段AB的三等分点？
(3)若点C是线段AB的中点，点M以每秒3个单位长度的速度从点C开始向右运动，同时点P以每秒5个单位长度的速度从点A出发向右运动，点N以每秒4个单位长度的速度从点B开始向左运动，点P与点M之间的距离表示为PM，点P与点N之间的距离表示为PN，是否存在某一时刻使得PM+PN=12？若存在，请求出此时点P表示的数；若不存在，请说明理由.
相关试题
