【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
参考答案:
【答案】B
【解析】
设巡逻船从出发到成功拦截所用时间为x小时,由题意得出∠ABC=120°,AB=12,BC=10x,AC=14x,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,由三角函数得出BD、AD的长度,得出CD=10x+6.在Rt△ACD中,由勾股定理得出方程,解方程即可.
解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=ABcos60°=![]() AB=6,AD=ABsin60°=
AB=6,AD=ABsin60°=![]() ,
,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得: ![]()
解得:![]() (不合题意舍去).
(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于南开(融侨)中学旁边的“转转桥”是重庆市网红景点之一,在桥下人形天桥(如图1),其平面图如图2所示,天桥入口D点有一台阶DC,CD=0.5米,其坡度为i=1:0.75,在DC上方有一平层BC=1米,且BC与地面MN平行,在天桥顶端A点测得B点的俯角为63°,且AD⊥MN,为知道台阶AB的长度,请根据以上信息,帮小亮计算出台阶AB的长度,约为( )精确到0.1米,参考数据:sin63°≈0.90,cos63°≈0.45,tan63°≈2.00

A. 1.4米 B. 2.5米 C. 2.8米 D. 2.9米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b
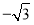 )2=0.
)2=0.(1)求a,b的值;
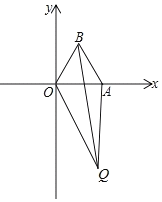
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°, ∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,又分别以M、N为圆心,大于
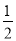 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.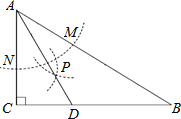
求证:(1)点D在AB的中垂线上.
(2)当CD=2时,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
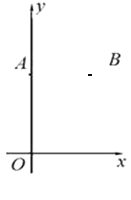
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:
①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:
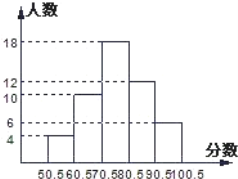
(1)该班共有多少名学生参加这次测验?
(2)求60.5~70.5这一分数段的频数是多少,频率是多少?
(3)若80分以上为优秀,则该班的优秀率是多少?
-
科目: 来源: 题型:
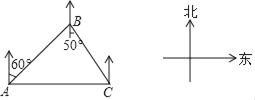
查看答案和解析>>【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=
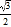 ;
;④∠ACB=50°.其中错误的是( )
A. ①② B. ②④ C. ①③ D. ③④
相关试题

