【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C. 
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标.
参考答案:
【答案】
(1)解:∵二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),
∴ ![]() ,
,
解得 ![]() ,
,
∴二次函数的解析式为:y=﹣x2+2x+3,顶点D的坐标为(1,4)
(2)解:如图所示,
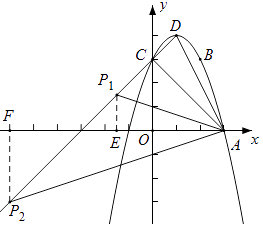
在y=﹣x2+2x+3中,当x=0时,y=3,
∴C(0,3)
∵A(3,0),D(1,4),
∴CD= ![]() ,AC=3
,AC=3 ![]() ,AD=2
,AD=2 ![]() ,
,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,且∠ACD=90°,
∴sin∠ACD= ![]() =
= ![]() =
= ![]()
(3)解:∵直线CD经过C(0,3),D(1,4),
∴设可设直线CD为y=kx+b,则
![]() ,
,
解得 ![]() ,
,
∴直线CD为y=x+3,
设点P的坐标为(a,a+3),
①如图所示,当点P在x轴上方时,过点P作PE⊥x轴于E,则
PE=a+3,AE=3﹣a,
∵∠AEP=∠ACD=90°,∠PAO=∠CAD,
∴△ACD∽△AEP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得a=﹣ ![]() ,
,
∴a+3= ![]() ,
,
∴此时P的坐标为(﹣ ![]() ,
, ![]() );
);
②如图所示,当点P在x轴下方时,过点P作PF⊥x轴于F,则
PF=﹣(a+3),AF=3﹣a,
∵∠AFP=∠ACD=90°,∠PAO=∠CAD,
∴△ACD∽△AFP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得a=﹣6,
∴a+3=﹣3,
∴此时P的坐标为(﹣6,﹣3);
综上所述,点P的坐标为 ![]()
【解析】(1)根据二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),求得m和n的值即可;(2)根据A,C,D三点的坐标,求得CD= ![]() ,AC=3
,AC=3 ![]() ,AD=2
,AD=2 ![]() ,得到CD2+AC2=AD2 , 根据勾股定理的逆定理得出△ACD是直角三角形,且∠ACD=90°,据此求得∠CAD的正弦值;(3)先求得直线CD为y=x+3,再设点P的坐标为(a,a+3),然后分两种情况进行讨论:当点P在x轴上方时,过点P作PE⊥x轴于E;当点P在x轴下方时,过点P作PF⊥x轴于F,分别判定△ACD∽△AEP,△ACD∽△AFP,列出比例式求得a的值即可.
,得到CD2+AC2=AD2 , 根据勾股定理的逆定理得出△ACD是直角三角形,且∠ACD=90°,据此求得∠CAD的正弦值;(3)先求得直线CD为y=x+3,再设点P的坐标为(a,a+3),然后分两种情况进行讨论:当点P在x轴上方时,过点P作PE⊥x轴于E;当点P在x轴下方时,过点P作PF⊥x轴于F,分别判定△ACD∽△AEP,△ACD∽△AFP,列出比例式求得a的值即可.
【考点精析】掌握勾股定理的逆定理和相似三角形的判定与性质是解答本题的根本,需要知道如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.

(1)如果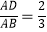 ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据
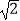 ≈1.41,
≈1.41, 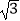 ≈1.73.
≈1.73. 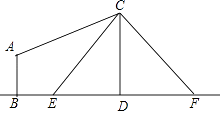
-
科目: 来源: 题型:
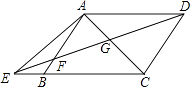
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且
 =
=  .
. 
(1)求证:AB∥CD;
(2)如果AD2=DGDE,求证: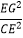 =
= 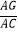 .
. -
科目: 来源: 题型:
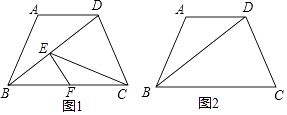
查看答案和解析>>【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC=
 .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= 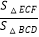 .
.
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一张直角三角形纸片ABC,∠C=90°,AB=24,tanB=
 (如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为 .
(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为 . 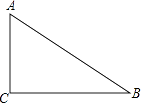
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=


求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
相关试题

