搜索
【题目】如图，已知在四边形ABCD中，AD∥BC，E为边CB延长线上一点，联结DE交边AB于点F，联结AC交DE于点G，且 
= 
． 
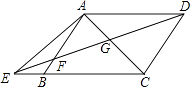
（1）求证：AB∥CD；
（2）如果AD2=DGDE，求证： 
= 
．
参考答案：
【答案】
（1）证明：∵AD∥BC，
∴△ADG∽△CEG，
∴ 
，
∵ 
= 
，
∴ 
，
∴AB∥CD
（2）证明：∵AD∥BC，
∴△ADG∽△CEG，
∴ 
，
∴ 
= 
，
∴ 
= 
，
∵AD2=DGDE，
∴ = 
，
∵AD∥BC，
∴ 
= ，
∴ = ．
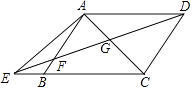
【解析】（1）由AD∥BC，得到△ADG∽△CEG，根据相似三角形的性质即可得到结论；（2）根据平行线的性质得到 ，根据等式的性质得到 = ，等量代换即可得到结论．
-
科目： 来源： 题型：
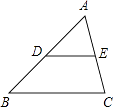
查看答案和解析>>【题目】如图，在△ABC中，点D，E分别是边AB，AC的中点，设
= 
， 
= 
． 
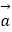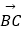（1）求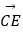向量
（用向量 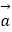， 的式子表示）．
（2）在图中作出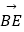向量
在向量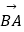 
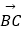， 方向上的分向量（不要求写作法，但要指出所作图中表示结论的向量）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点D是AB边上一点，过点D作DE∥BC，交AC于E，点F是DE延长线上一点，联结AF．
（1）如果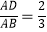
，DE=6，求边BC的长；
（2）如果∠FAE=∠B，FA=6，FE=4，求DF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，电线杆CD上的C处引拉线CE，CF固定电线杆，在离电线杆6米的B处安置测角仪（点B，E，D在同一直线上），在A处测得电线杆上C处的仰角为30°，已知测角仪的高AB=1.5米，BE=2.3米，求拉线CE的长，（精确到0.1米）参考数据
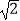≈1.41， 
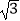≈1.73．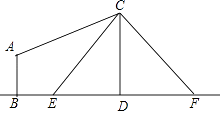 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在平面直角坐标系xOy中，二次函数y=﹣x2+mx+n的图象经过点A（3，0），B（m，m+1），且与y轴相交于点C．
（1）求这个二次函数的解析式并写出其图象顶点D的坐标；
（2）求∠CAD的正弦值；
（3）设点P在线段DC的延长线上，且∠PAO=∠CAD，求点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在梯形ABCD中，AD∥BC，AB=AD=5，tan∠DBC=
．点E为线段BD上任意一点（点E与点B，D不重合），过点E作EF∥CD，与BC相交于点F，连接CE．设BE=x，y=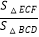 
．
（1）求BD的长；
（2）如果BC=BD，当△DCE是等腰三角形时，求x的值；
（3）如果BC=10，求y关于x的函数解析式，并写出自变量x的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】一张直角三角形纸片ABC，∠C=90°，AB=24，tanB=
（如图），将它折叠使直角顶点C与斜边AB的中点重合，那么折痕的长为 ． 
相关试题
