【题目】如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.
(1)求证:GF=BF;
(2)若△ABC的边长为a,BE的长为b,且a,b满足(a﹣7)2+b2﹣6b+9=0,求BF的长.

参考答案:
【答案】(1)见解析;(2)2
【解析】
(1)由DG∥BE得到∠GDF=∠E,则可根据“AAS”判定△FDG≌△FEB,则GF=BF;
(2)利用配方法得(a-7)2+(b-3)2=0,则根据非负数的性质得到a-7=0,b-3=0,解得a=7,b=3,即BE=3,BC=7,所以DG=BE=3,由于DG∥AB,△ABC是等边三角形,则△CDG为等边三角形,所以CG=DG=3,可计算出BG=BC-CG=4,然后利用GF=BF可得到BF的长.
(1)证明:∵DG∥BE,
∴∠GDF=∠E,
在△FDG和△FEB中, ,
,
∴△FDG≌△FEB(AAS),
∴GF=BF;
(2)∵(a-7)2+b2-6b+9=0,
∴(a-7)2+(b-3)2=0,
∴a-7=0,b-3=0,解得a=7,b=3,
∴BE=3,BC=7,
∴DG=BE=3,
∵DG∥AB,
∴△CDG为等边三角形,
∴CG=DG=3,
∴BG=BC-CG=4,
而GF=BF,
∴BF=![]() BG═2.
BG═2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
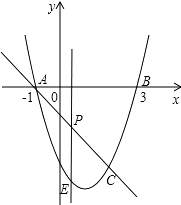
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,(不与A、C重合),过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值,并直接写出△ACE面积的最大值;
(3)点G为抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的F点坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F等于( )
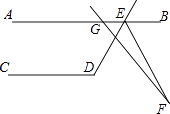
A.9.5°
B.19°
C.15°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
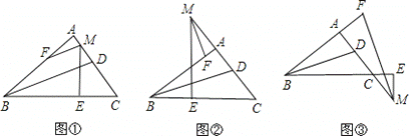
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC沿射线BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,则图中阴影部分的面积为__________.
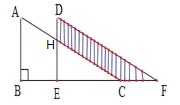
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎解方理
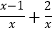 =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
(1)小马虎解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
相关试题

