搜索
【题目】如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F等于（ ）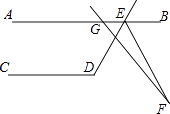 
A.9.5°
B.19°
C.15°
D.30°
参考答案：
【答案】A
【解析】解：∵AB∥CD，∠CDE=119°， ∴∠AED=180°﹣119°=61°，∠DEB=119°．
∵GF交∠DEB的平分线EF于点F，
∴∠DEF= 
×119°=59.5°，
∴∠GEF=61°+59.5°=120.5°．
∵∠AGF=130°，
∴∠F=∠AGF﹣∠GEF=130°﹣120.5°=9.5°．
故选：A．
【考点精析】本题主要考查了角的平分线和平行线的性质的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）
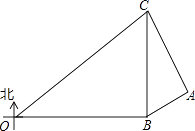
（1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？
（2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？
（3）若敌舰A沿最短距离的路线以20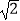
海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？ -
科目： 来源： 题型：
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1)，然后将剩余部分拼成一个长方形(如图2).
(1)探究：上述操作能验证的等式是 ；(请选择正确的一个)
A．a2-2ab+b2=(a-b)2 B．a2-b2=(a+b)(a-b)
C．a2+ab=a(a+b)
(2)应用：利用你从(1)选出的等式，完成下列各题：
①已知9x2-4y2=24，3x+2y=6，求3x-2y的值；
②计算：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2﹣2x﹣3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．
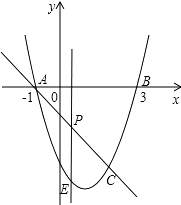
（1）求A、B两点的坐标及直线AC的函数表达式；
（2）P是线段AC上的一个动点，（不与A、C重合），过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值，并直接写出△ACE面积的最大值；
（3）点G为抛物线上的动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的F点坐标；如果不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）如图①，M为边AC上一点，则BD、MF的位置关系是 ；
如图②，M为边AC反向延长线上一点，则BD、MF的位置关系是 ；
如图③，M为边AC延长线上一点，则BD、MF的位置关系是 ；
（2）请就图①、图②、或图③中的一种情况，给出证明.
-
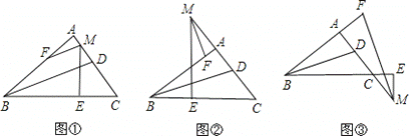
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC是等边三角形，D为AC边上的一点，DG∥AB，延长AB到E，使BE=GD，连接DE交BC于F．
(1)求证：GF=BF；
(2)若△ABC的边长为a，BE的长为b，且a，b满足(a﹣7)2+b2﹣6b+9=0，求BF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将Rt△ABC沿射线BC方向平移得到△DEF，已知AB=16cm，BE=10cm，DH=6cm，则图中阴影部分的面积为__________．
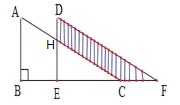
相关试题
