【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当
与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当![]() 的周长值最小时,则这个最小值是_______.
的周长值最小时,则这个最小值是_______.

参考答案:
【答案】![]()
![]()
【解析】
如图(见解析),先根据一次函数的解析式可得点A、B的坐标,从而可得OA、OB、AB的长,再根据正方形的性质可得![]() ,
,![]() ,然后根据三角形全等的判定定理与性质可得
,然后根据三角形全等的判定定理与性质可得![]() ,由此即可得出点D的坐标;同样的方法可求出点C的坐标,再根据轴对称的性质可得点
,由此即可得出点D的坐标;同样的方法可求出点C的坐标,再根据轴对称的性质可得点![]() 的坐标,然后根据轴对称的性质和两点之间线段最短得出
的坐标,然后根据轴对称的性质和两点之间线段最短得出![]() 的周长值最小时,点M的位置,最后利用两点之间的距离公式、三角形的周长公式即可得.
的周长值最小时,点M的位置,最后利用两点之间的距离公式、三角形的周长公式即可得.
如图,过点D作![]() 轴于点E,作点C关于y轴的对称点
轴于点E,作点C关于y轴的对称点![]() ,交y轴于点F,连接
,交y轴于点F,连接![]() ,交y轴于点
,交y轴于点![]() ,连接
,连接![]() ,则
,则![]() 轴
轴
对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点A的坐标为
,则点A的坐标为![]()
当![]() 时,
时,![]() ,则点B的坐标为
,则点B的坐标为![]()
![]()
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]() ,
,![]()
![]()
![]()
在![]() 和
和![]() 中,
中,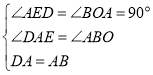
![]()
![]()
![]()
则点D的坐标为![]()
同理可证:![]()
![]()
![]()
则点C的坐标为![]()
由轴对称的性质得:点![]() 的坐标为
的坐标为![]() ,且
,且![]()
![]() 的周长为
的周长为![]()
由两点之间线段最短得:当点M与点![]() 重合时,
重合时,![]() 取得最小值
取得最小值![]()
![]()
![]()
则![]() 的周长的最小值为
的周长的最小值为![]()
故答案为:![]() ,
,![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  ,将
,将 绕点
绕点 沿逆时针方向旋转
沿逆时针方向旋转 得到
得到 .
.
(1)线段
 的长是 ,
的长是 ,  的度数是 ;
的度数是 ;(2)连结
 ,求证:四边形
,求证:四边形 是平行四边形;
是平行四边形;(3)求四边形
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等边
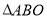 的顶点
的顶点 在
在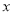 轴的负半轴上,点
轴的负半轴上,点 的坐标为
的坐标为 ,则点
,则点 坐标为_______;点
坐标为_______;点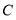 是位于
是位于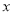 轴上点
轴上点 左边的一个动点,以
左边的一个动点,以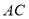 为边在第三象限内作等边
为边在第三象限内作等边 ,若点
,若点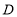
 .小明所在的数学兴趣合作学习小组借助于现代互联网信息技术,课余时间经过探究发现无论点
.小明所在的数学兴趣合作学习小组借助于现代互联网信息技术,课余时间经过探究发现无论点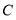 在点
在点 左边
左边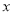 轴负半轴任何位置,
轴负半轴任何位置, ,
, 之间都存在着一个固定的一次函数关系,请你写出这个关系式是_____.
之间都存在着一个固定的一次函数关系,请你写出这个关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为
 小时.
小时.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川苍溪小王家今年红心猕猴桃喜获丰收,采摘上市20天全部销售完,小王对销售情况进行跟踪记录,并将记录情况绘制成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图(1)所示,红星猕猴桃的价格z(单位:元/千克)与上市时间x(天)的函数关系式如图(2)所示.

(1)观察图象,直接写出日销售量的最大值;
(2)求小王家红心猕猴桃的日销量y与上市时间x的函数解析式;并写出自变量的取值范围.
(3)试比较第6天和第13天的销售金额哪天多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老汉为了与顾客签订购销合同,对自己鱼塘中鱼的总质量进行了估计,第一次捞出100条,称得质量为184千克.并将每条鱼做上记号后放入水中,当它们完全混合于鱼群后,又捞出200条,称得质量为416千克,且带有记号的鱼有20条,王老汉的鱼塘中估计有鱼多少条鱼?总质量为多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明你的结论;
(2)连接DE,如图②,求证:BD2+CD2=2AD2
(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=
 ,CD=1,则AD的长为 ▲ .(直接写出答案)
,CD=1,则AD的长为 ▲ .(直接写出答案)
相关试题

