【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,将
,将![]() 绕点
绕点![]() 沿逆时针方向旋转
沿逆时针方向旋转![]() 得到
得到![]() .
.

(1)线段![]() 的长是 ,
的长是 , ![]() 的度数是 ;
的度数是 ;
(2)连结![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(3)求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)6, 135度;(2)详见解析;(3)36.
【解析】试题分析:(1)图形在旋转过程中,边长和角的度数不变;
(2)可证明OA∥A1B1且相等,即可证明四边形OAA1B1是平行四边形;
(3)利用弧长公式求得点B划过的弧长即可.
试题解析:(1)解:因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°.
(2)证明:∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3)36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司有三个住宅区,A,B,C各区分别住有职工10人,15人,45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=150m,BC=90m.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点AB. 点BC. 点A,B之间D. 点C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等边
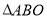 的顶点
的顶点 在
在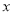 轴的负半轴上,点
轴的负半轴上,点 的坐标为
的坐标为 ,则点
,则点 坐标为_______;点
坐标为_______;点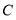 是位于
是位于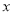 轴上点
轴上点 左边的一个动点,以
左边的一个动点,以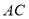 为边在第三象限内作等边
为边在第三象限内作等边 ,若点
,若点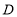
 .小明所在的数学兴趣合作学习小组借助于现代互联网信息技术,课余时间经过探究发现无论点
.小明所在的数学兴趣合作学习小组借助于现代互联网信息技术,课余时间经过探究发现无论点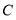 在点
在点 左边
左边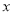 轴负半轴任何位置,
轴负半轴任何位置, ,
, 之间都存在着一个固定的一次函数关系,请你写出这个关系式是_____.
之间都存在着一个固定的一次函数关系,请你写出这个关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为
 小时.
小时.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
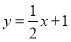 与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当
与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当 的周长值最小时,则这个最小值是_______.
的周长值最小时,则这个最小值是_______.
相关试题

