【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(4,8).
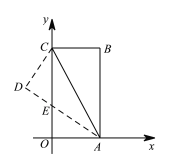
(1)△AEC是等腰三角形吗?请证明;
(2)求点D的横坐标.
参考答案:
【答案】(1)详见解析;(2)D(-![]() ,
,![]() ).
).
【解析】
(1)由翻折可知∠BAC=∠DAC,由OC∥AB可得∠OCA=∠BAC,所以∠EAC=∠ACE,即可证明△AEC是等腰三角形;
(2) 首先过点D作DF⊥OA于F,由四边形OABC是矩形与折叠的性质,易证得△AEC是等腰三角形,然后在Rt△AEO中,利用勾股定理求得AE,OE的长,然后等积求高法得DF的长,利用勾股定理得EF得长,即可得点D的横坐标.
⑴证明:由翻折可知,∠BAC=∠DAC,∵OC∥AB,∴∠OCA=∠BAC,
∴∠EAC=∠ACE,∴AE=CE,即△AEC是等腰三角形.
⑵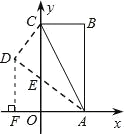
如图,过点D作DF⊥x轴于F,由(1),令AE=CE=x,则OE=8-x,
在Rt△OEA中,由勾股定理,(8-x)2+42=x2,
解得x=5,∴AE=CE=5,OE=DE=3,在Rt△CDE中,由等积求高法,得DF=![]() ,
,
利用勾股定理,EF=![]() ,于是OF=3+
,于是OF=3+![]() =
=![]() ,DF=
,DF=![]() ,
,
∴D(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点B在x轴上,且
,点B在x轴上,且 .
. 求点B的坐标;
求点B的坐标; 求
求 的面积;
的面积; 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系 xOy 中,A(2,3),B(3,1),C(﹣2,﹣1).
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1,B1,C1 的坐标;
②在 y 轴上画出点 P,使 PA+PB 最小.(不写作法,保留作图痕迹)
③求△ABC 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:BD为
 的直径,O为圆心,点A为圆上一点,过点B作
的直径,O为圆心,点A为圆上一点,过点B作 的切线交DA的延长线于点F,点C为
的切线交DA的延长线于点F,点C为 上一点,且
上一点,且 ,连接BC交AD于点E,连接AC.
,连接BC交AD于点E,连接AC. 如图1,求证:
如图1,求证: ;
; 如图2,点H为
如图2,点H为 内部一点,连接OH,CH若
内部一点,连接OH,CH若 时,求证:
时,求证: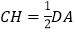 ;
; 在
在 的条件下,若
的条件下,若 ,
, 的半径为10,求CE的长.
的半径为10,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某地特色农产品在国际市场上颇具竞争力,其中绿色蔬菜远销日本和韩国等地
 上市时,若按市场价格10元
上市时,若按市场价格10元 千克在新区收购了2000千克绿色蔬菜存放入冷库中
千克在新区收购了2000千克绿色蔬菜存放入冷库中 据预测,绿色蔬菜的市场价格每天每千克将上涨
据预测,绿色蔬菜的市场价格每天每千克将上涨 元,但冷库存放这批绿色蔬菜时每天需要支出各种费用合计340元,而且绿色蔬菜在冷库中最多保存110天,同时,平均每天有6千克的绿色蔬菜损坏不能出售.
元,但冷库存放这批绿色蔬菜时每天需要支出各种费用合计340元,而且绿色蔬菜在冷库中最多保存110天,同时,平均每天有6千克的绿色蔬菜损坏不能出售. 若存放x天后,将这批绿色蔬菜一次性出售,设这批绿色蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.
若存放x天后,将这批绿色蔬菜一次性出售,设这批绿色蔬菜的销售总金额为y元,试写出y与x之间的函数关系式. 这批绿色蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
这批绿色蔬菜存放多少天后出售可获得最大利润?最大利润是多少?
相关试题

