【题目】作图题:如图,在平面直角坐标系 xOy 中,A(2,3),B(3,1),C(﹣2,﹣1).
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1,B1,C1 的坐标;
②在 y 轴上画出点 P,使 PA+PB 最小.(不写作法,保留作图痕迹)
③求△ABC 的面积.

参考答案:
【答案】①如图所示见解析, A1 的坐标(2,﹣3),B1 的坐标(3,﹣1),C1 的坐标(﹣2,1);②如图所示见解析;③6.
【解析】
①分别作出各点关于 x 轴的对称点,再顺次连接即可;根据各点在坐标系中的位置写出各点坐标即可;②作点 A 关于 y 轴的对称点 A',连接 A'B 交 y 轴于点 P,点 P 即为所求;③利用割补法即可求得△ABC的面积.
①如图所示,△A1B1C1 即为所求;A1 的坐标(2,﹣3),B1 的坐标(3,﹣1),C1 的坐标(﹣2,1);
②如图所示,点 P 即为所求;

③S△ABC=S△ABD+S△BCD=![]() ×3×2+
×3×2+![]() ×3×2=6.
×3×2=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于
 BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )
BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( ) 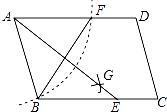
A.11
B.6
C.8
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=
 ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 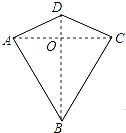
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
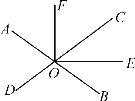
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE是∠COB的平分线,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度数;
(2)OF是∠AOC的平分线吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料并解答下列问题.
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.

-
科目: 来源: 题型:
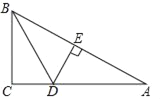
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,DE垂直平分AB,垂足为E,若BC=3,则AD的长为( )
A.
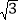 B. 2 C. 2
B. 2 C. 2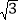 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
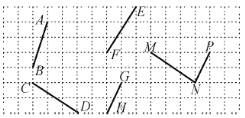
相关试题

