搜索
【题目】已知：BD为
的直径，O为圆心，点A为圆上一点，过点B作的切线交DA的延长线于点F，点C为上一点，且
，连接BC交AD于点E，连接AC．
如图1，求证：
；
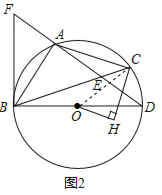
如图2，点H为内部一点，连接OH，CH若
时，求证：
；
在的条件下，若
，的半径为10，求CE的长．
参考答案：
【答案】(1)见解析；（2）见解析；（3）
.
【解析】
由BD为
的直径，得到
，根据切线的性质得到
，根据等腰三角形的性质得到
，等量代换即可得到结论；
如图2，连接OC，根据平行线的判定和性质得到
，根据等腰三角形的性质得到
，
，根据相似三角形的性质即可得到结论；
根据相似三角形的性质得到
，根据勾股定理得到
，根据全等三角形的性质得到
，
，根据射影定理得到
，根据相交弦定理即可得到结论．
为
的直径，
，
，
是的切线，
，
，
，
，
，
，
；
如图2，连接OC，
，
，
，
，
，
，
即
，
，
，
∽
，
，
；
由知，
∽，
，
，的半径为10，
，
，
，
在
与
中，
，
≌，
，
，
，
，
，
，
，
，
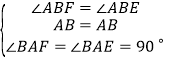，BC交于E，
，
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点A1(1，1)，第二次向右跳动3个单位至点A2(2，1)，第三次跳动至点A3(2，2)，第四次向右跳动5个单位至点A4(3，2)，…，以此规律跳动下去，点A第100次跳动至点A100的坐标是（）
A.(50，50)B.(51，51)C.(51，50)D.(50，51)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，点B在x轴上，且
．
求点B的坐标；
求
的面积；
在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题：如图，在平面直角坐标系 xOy 中，A（2，3），B（3，1），C（﹣2，﹣1）．
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1，B1，C1 的坐标；
②在 y 轴上画出点 P，使 PA+PB 最小．（不写作法，保留作图痕迹）
③求△ABC 的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把长方形纸片OABC放入平面直角坐标系中，使OA，OC分别落在x轴、y轴上，连接AC，将纸片OABC沿AC折叠，使点B落在点D的位置，AD与y轴交于点E，若B(4，8).
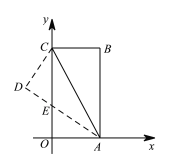
(1)△AEC是等腰三角形吗?请证明；
(2)求点D的横坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把矩形纸片ABCD沿对角线折叠，设重叠部分为△EBD，那么下列说法错误的是（ ）
A. △EBD是等腰三角形，EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．
恒成立的结论有 ．（把你认为正确的序号都填上）
相关试题
