【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
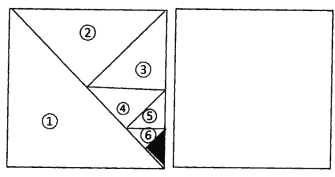
(1)阴影部分的面积是多少?
(2)受此启发,你能求出![]() 的值吗?
的值吗?
(3)请你利用图中右侧的正方形,再设计能求![]() 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)
(4)根据以上规律,![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(2)见解析;(4)
;(2)见解析;(4)![]()
【解析】
(1)阴影部分的面积等于部分⑥的面积;
(2)用整个正方形的面积减去阴影部分的面积即可确定答案;
(3)依照题目的示范作图即可;
(4)用整个正方形的面积减去阴影部分的面积即可确定答案.
(1)∵部分①是整体面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,
∴图中阴影部分的面积是部分⑤的一半,即![]() ,
,
故答案为:![]() ;
;
(2)![]() ;
;
(3)如图所示(彩色部分)即为:求![]() 的值的几何图形.
的值的几何图形.
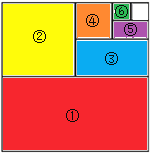
(4)![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
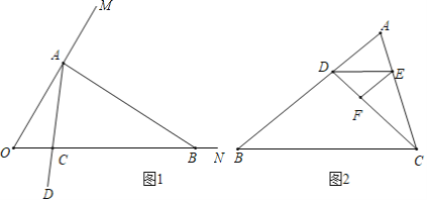
概念理解:如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为______,△AOB______(填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:(3)如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
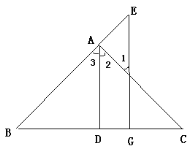
理由如下:
 AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( ) AD‖EG,( )
AD‖EG,( ) ∠1=∠2,( )
∠1=∠2,( )=∠3,(两直线平行,同位角相等)
又
 ∠E=∠1(已知)
∠E=∠1(已知) = (等量代换)
= (等量代换)  AD平分∠BAC( )
AD平分∠BAC( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=
 (∠A+∠C).
(∠A+∠C).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,m)在双曲线y=
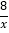 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=
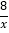 经过点C,求t的值.
经过点C,求t的值.(2)如图2,将图1中的双曲线y=
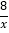 (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣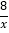 (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣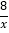 (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.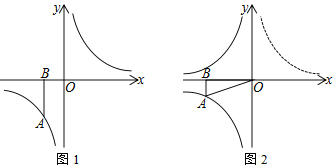
相关试题

