【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

参考答案:
【答案】5 ![]()
【解析】
①过D作DP⊥AB于P,,则△ADP是等腰直角三角形,根据等腰直角三角形的性质得到![]() ,进而求得AP=DP=5;
,进而求得AP=DP=5;
②作点O关于AB的对称点M,点O关于AD的对称点N,连接MN交AB于F交AD于E,则△OEF周长的最小, △OEF周长的最小值=MN,由作图得: AN=AO=AM, ∠NAD=∠DAO, ∠MAB=∠BAO,于是得到![]() .根据三角形的中位线的性质得到
.根据三角形的中位线的性质得到![]() ,
,![]() ,根据勾股定理得到
,根据勾股定理得到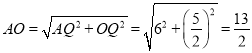 ,然后根据等腰直角三角形的性质即可得到结论.
,然后根据等腰直角三角形的性质即可得到结论.
①过D作DP⊥AB于P,
则A△DP是等腰直角三角形,![]() ,
,
![]() ,
,
∴AP=DP=sin45°×5![]() =5;
=5;
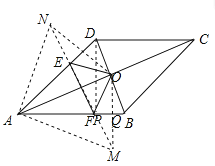
②作点O关于AB的对称点M,点O关于AD的对称点N,连接MN交AB于F交AD于E,则△OEF周长的最小, △OEF周长的最小值=MN,
由作图得:AN=AO=AM, ∠NAD=∠DAO, ∠MAB=∠BAO,
![]() ,
,
![]() ,
,
∵OM⊥AB于Q,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,![]() ,
,
![]()
∴△OEF周长的最小值是![]() .
.
故答案为①5;② ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
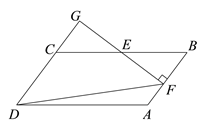
(1)求证:GD=GF.
(2)已知BC=10,
 .求 CD的长.
.求 CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(-3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)若A(-2,y1),B(5,y2)是抛物线y=2x2+bx+1上的两点,试比较y1与y2的大小关系;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位长度,使平移后的图象与x轴无交点,求k的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=_____.
-
科目: 来源: 题型:
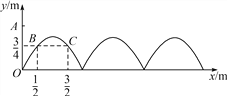
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为
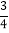 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为 m,
m, m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图所示.
第四步:计算大正方形面积用x表示为 .长方形面积为常数 .小正方形面积为常数 .
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程 ,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入 ; ; ; .
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程x2﹣x﹣1=0.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DEF:∠EFH=3:2,∠1=∠B,∠2+∠3=180°,求∠DEF的度数.

相关试题

