【题目】已知P(-3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)若A(-2,y1),B(5,y2)是抛物线y=2x2+bx+1上的两点,试比较y1与y2的大小关系;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位长度,使平移后的图象与x轴无交点,求k的最小值.
参考答案:
【答案】(1)b=4;(2)y1<y2;(3)k的最小值为2
【解析】试题分析: (1)由于点![]() 是二次函数
是二次函数![]() 图象上的两点,故可得抛物线对称轴是直线
图象上的两点,故可得抛物线对称轴是直线![]() 故
故![]() 即可得到
即可得到![]() 的值;
的值;
(2)将![]() 两点坐标分别代入抛物线求出
两点坐标分别代入抛物线求出![]() 的值,即可比较大小;
的值,即可比较大小;
(3)利用二次函数图象的平移规律,可得平移后抛物线的关系式为![]() 要使平移后图象与
要使平移后图象与![]() 轴无交点,即
轴无交点,即![]() 无解,根据一元二次方程的根的判别式可得
无解,根据一元二次方程的根的判别式可得![]() 求出
求出![]() 的取值范围,结合
的取值范围,结合![]() 为正整数即可解答题目.
为正整数即可解答题目.
试题解析: (1)∵点![]() 是二次函数
是二次函数![]() 图象上的两点,
图象上的两点,
∴此抛物线的对称轴是直线![]()
∵二次函数的表达式为![]()
∴![]() 解得
解得![]()
(2) 将![]() 两点坐标分别代入抛物线得
两点坐标分别代入抛物线得
![]()
![]()
![]()
(3)平移后抛物线的表达式为![]()
要使平移后的图象与![]() 轴无交点,
轴无交点,
即![]() 无解,
无解,
则有![]()
解得![]()
∵![]() 是正整数,∴
是正整数,∴![]() 的最小值为2.
的最小值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
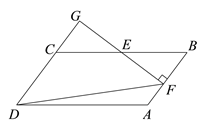
(1)求证:GD=GF.
(2)已知BC=10,
 .求 CD的长.
.求 CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5
 ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为
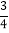 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为 m,
m, m.
m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
相关试题

