【题目】在ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=_____.
参考答案:
【答案】7或3
【解析】
分AE与DF的交点在矩形内和矩形外两个情况讨论,利用勾股定理可求的AB的值.
解:①如图: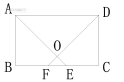
当AE与DF的交点为O点,当O在矩形内时,
在□ABCD中,由AE平分∠BAD交边BC于E,DF⊥AE,
易得:△ABE、△AOD、△OEF均为等要直角三角形,
在RT△ABE中,设AB=x,可得AE=![]() =
=![]() x,
x,
在RT△OEF中由EF=4,可得OE=![]() ,
,
![]() AO=AE-OE=
AO=AE-OE=![]() x-
x-![]() ,
,
在RT△AOD中,可得AD=![]() AO,
AO,
即:10=![]()
![]() (
(![]() x-
x-![]() ),10=2x-4,x=7;
),10=2x-4,x=7;
②如图: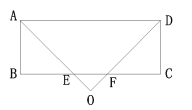
同理可得,设AB=x,AE=![]() =
=![]() x,OE=
x,OE=![]()
![]() AO=AE+OE=
AO=AE+OE=![]() x+
x+![]() ,AD=
,AD=![]() AO,
AO,
可得:10=![]()
![]() (
(![]() x+
x+![]() ),10=2x+4,x=3;
),10=2x+4,x=3;
综合所述:x=7或x=3;
故答案:7或3.
-
科目: 来源: 题型:
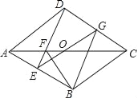
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.
-
科目: 来源: 题型:
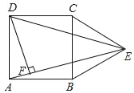
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
-
科目: 来源: 题型:
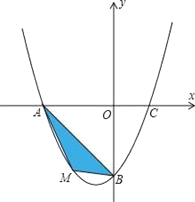
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线
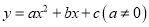 与x轴相交于
与x轴相交于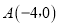 ,C两点
,C两点 与y轴相交于点B
与y轴相交于点B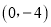 .
.
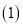 a0,
a0, 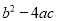
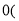 填“
填“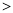 ”或“
”或“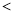 ”
” 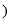 ;
; 若该抛物线关于直线
若该抛物线关于直线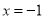 对称,求抛物线的函数表达式;
对称,求抛物线的函数表达式;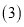 在
在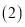 的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为
的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为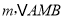 的面积为
的面积为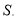 求S关于m的函数关系式,并求出S的最大值;
求S关于m的函数关系式,并求出S的最大值;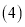 在
在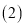 的条件下,若点P是抛物线上的动点,点Q是直线
的条件下,若点P是抛物线上的动点,点Q是直线 上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由自己租车运回,已知该公司租车从基地到公司的运输费用为5000元
(1)分别写出该公司两种购买方案付款金额
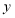 (元)与所购的水果
(元)与所购的水果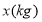 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.(2)依据购买量判断,选择哪种方案付款少?并说理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,一次函数

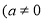 )和二次函数
)和二次函数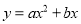
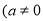 )的图象可能为( )
)的图象可能为( )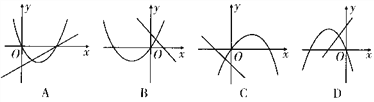
A. A B. B C. C D. D
相关试题

