【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=__________°;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.

参考答案:
【答案】(1)∠BDC=∠A+∠B+∠C;(2)①40°;②∠DCE=90°;③∠A =70°.
【解析】试题分析:(1)、连接AD并延长至点F,根据外角的性质得出∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,从而得出我们所需要的结论;(2)、①、根据第一题的结论得出答案;②、根据第一题的结论得出∠ADB+∠AEB=80°,然后根据∠DCE=![]() (∠ADB+∠AEB)+∠A得出答案;③、根据题意得出∠BG1C=
(∠ADB+∠AEB)+∠A得出答案;③、根据题意得出∠BG1C=![]() (∠ABD+∠ACD)+∠A,然后设∠A为x°,根据∠ABD+∠ACD=140°-x°得出答案.
(∠ABD+∠ACD)+∠A,然后设∠A为x°,根据∠ABD+∠ACD=140°-x°得出答案.
试题解析:(1)、连接AD并延长至点F,由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD;相加可得∠BDC=∠A+∠B+∠C;
(2)、①、由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC, 又因为∠A=50°,∠BXC=90°,
所以∠ABX+∠ACX=90°-50°=40°;
②、由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;
而∠DCE=![]() (∠ADB+∠AEB)+∠A, 代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
(∠ADB+∠AEB)+∠A, 代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
③、∠BG1C=![]() (∠ABD+∠ACD)+∠A, ∵∠BG1C=77°, ∴设∠A为x°,
(∠ABD+∠ACD)+∠A, ∵∠BG1C=77°, ∴设∠A为x°,
∵∠ABD+∠ACD=140°-x° ∴![]() (140-x)+x=77,x=70 ∴∠A为70°.
(140-x)+x=77,x=70 ∴∠A为70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一副三角板可以画出的最大锐角的度数是( )
A. 85° B. 75° C. 60° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明根据的是等式的哪一条性质以及是怎样变形的.
(1)如果
 ,那么x=__________,根据____________________;
,那么x=__________,根据____________________;(2)如果-2x=2y,那么x=_________,根据____________________;
(3)如果x=3x+2,那么x-_______=2,根据____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4x=9+x;
(2)4-
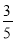 m=7;
m=7;(3)8y-3=5y+3;
(4)4x+5=3x+3-2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,否则每超过1天罚款1 000元,甲、乙两人经商量后签订了该合同.
(1)正常情况下,甲、乙两人能否履行该合同?为什么?
(2)现两人合作了这项工程的75%,因别处有急事,必须调走1人,问调走谁更合适些?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句错误的是( )
A. 两点确定一条直线
B. 同角的余角相等
C. 两点之间线段最短
D. 两点之间的距离是指连接这两点的线段
相关试题

