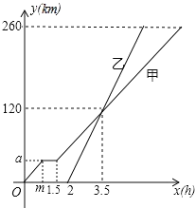
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)直接写出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x (h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车出发多长时间后,两车恰好相距40km?
参考答案:
【答案】(1)m=1,a=40,(2)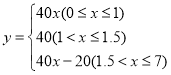 ;(3)
;(3)![]() 小时或
小时或![]() 小时.
小时.
【解析】
(1)根据“路程÷时间=速度”由函数图象就可以求出甲的速度求出a的值和m的值;
(2)由分段函数当0≤x≤1,1<x≤1.5,1.5<x≤7由待定系数法就可以求出结论;
(3)先求出乙车行驶的路程y与时间x之间的解析式,由解析式之间的关系建立方程求出其解即可.
(1)由题意,得
m=1.5-0.5=1.
120÷(3.5-0.5)=40,
∴a=40.
答:a=40,m=1;
(2)当0≤x≤1时设y与x之间的函数关系式为y=k1x,由题意,得
40=k1,
∴y=40x
当1<x≤1.5时,
y=40;
当1.5<x≤7设y与x之间的函数关系式为y=k2x+b,由题意,得
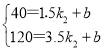 ,
,
解得:![]() ,
,
∴y=40x-20.
∴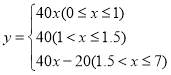 ;
;
(3)设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,由题意,得

解得: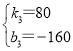 ,
,
∴y=80x-160.
当40x-20-40=80x-160时,
解得:x=![]() .
.
当40x-20+40=80x-160时,
解得:x=![]() .
.
![]() 2=
2=![]() ,
,![]() 2=
2=![]() .
.
答:乙车行驶![]() 小时或
小时或![]() 小时,两车恰好相距40km.
小时,两车恰好相距40km.
-
科目: 来源: 题型:
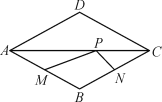
查看答案和解析>>【题目】点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°, 点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
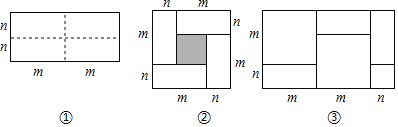
(1)图②中的阴影部分的面积为 .
(2)观察图②,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 .
(3)若x+y=﹣6,xy=
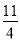 ,则x﹣y= .
,则x﹣y= .(4)观察图③,你能得到怎样的代数恒等式呢?
-
科目: 来源: 题型:
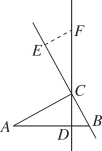
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
-
科目: 来源: 题型:
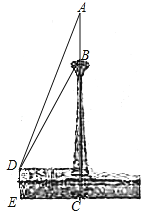
查看答案和解析>>【题目】如图所示,天津电视塔顶部有一桅杆部分AB,数学兴趣小组的同学在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求测得的桅杆部分AB的高度和电视塔AC的高度.(结果保留小数点后一位).
参考数据:tan67.3°≈2.39,tan60°≈1.73.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
(2)在同一直角坐标系中画出(1)中函数的图象;
(3)春节期间如何选择这两家商场去购物更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线
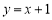 和x轴上,则点B2019的横坐标是______.
和x轴上,则点B2019的横坐标是______. 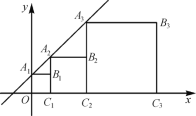
相关试题

