【题目】如图,△ABE为等腰直角三角形,∠ABE=90°,BC=BD,∠FAD=30°. 
(1)求证:△ABC≌△EBD;
(2)求∠AFE的度数.
参考答案:
【答案】
(1)证明:∵△ABE为等腰直角三角形,
∴AB=BE,
∵∠ABE=90°,
∴∠ABE=∠DBE=90°,
在△ABC与△BDE中,  ,
,
∴△ABC≌△EBD
(2)解:∵△ABC≌△EBD,
∴∠BAC=∠BED,
∵∠BED+∠D=90°,
∴∠BAC+∠D=90°,
∴∠AFD=90°,
∴∠AFE=90°
【解析】(1)根据等腰直角三角形的性质得到AB=BE,根据邻补角的定义得到∠ABE=∠DBE=90°,根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到∠BAC=∠BED,根据三角形的内角和得到∠BED+∠D=90°,等量代换得到∠BAC+∠D=90°,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.
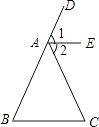
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
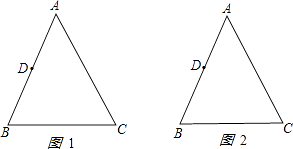
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等? -
科目: 来源: 题型:
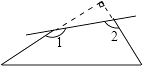
查看答案和解析>>【题目】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2等于( )
A.270°
B.180°
C.135°
D.90° -
科目: 来源: 题型:
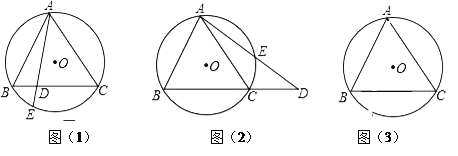
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB=AC,
(1)⊙O的弦AE交于BC于D.求证:ABAC=ADAE;
(2)在(1)的条件下当弦AE的延长线与BC的延长线相交于点D时,上述结论是否还成立?若成立,请给予证明.若不成立,请说明理由.
(3)已知⊙O 的半径2,∠ACB=40°,求BA的长.(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
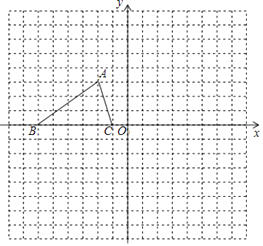
(1)将△ABC沿y轴翻折,则翻折后点A的对应点的坐标是 .
(2)作出△ABC关于y轴对称的图形△A1B1C1 , 画△A1B1C1 , 并直接写出点A1的坐标.
(3)将△ABC向下平移平移6个单位,向右平移7个单位得到△A2B2C2 , 画出平移后的图形.
(4)若以D,B,C为顶点的三角形与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.
相关试题

