【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
参考答案:
【答案】
(1)
MN=MC+NC= AC+ BC= (AC+BC)= ×(8+6)= ×14=7
(2)
MN=MC+NC= ![]() (AC+BC)=
(AC+BC)=![]() a
a
(3)
MN=MC-NC= AC- BC= (AC-BC)= b
(4)
如图,只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
【解析】(1)根据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半,那么MC、CN的和就应该是AC、BC和的一半,也就是说MN是AB的一半,有了AC、CB的值,那么就有了AB的值,也就能求出MN的值了;(2)方法同(1)只不过AC、BC的值换成了AC+CB=a cm,其他步骤是一样的;(3)当C在线段AB的延长线上时,根据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半.于是,MC、NC的差就应该是AC、BC的差的一半,也就是说MN是AC-BC即AB的一半.有AC-BC的值,MN也就能求出来了;(4)综合上面我们可发现,无论C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知□ABCD中,AB=8 cm,BC=7 cm,则此平行四边形的周长为_________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.h≤17
B.h≥8
C.15≤h≤16
D.7≤h≤16 -
科目: 来源: 题型:
查看答案和解析>>【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
(1)情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
(2)情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组式的变形过程,然后回答问题: 例1:
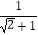 =
= 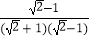 =
= 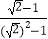 =
= 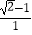 =
= 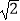 ﹣1.
﹣1.
例2: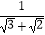 =
= 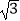 ﹣
﹣ 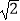 ,
, 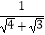 =
= 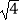 ﹣
﹣ 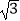 ,
, 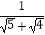 =
= 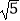 ﹣
﹣ 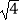
利用以上结论解答以下问题:
(1)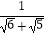 =;
=; 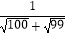 =;
=;
(2)你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)应用上面的结论,求下列式子的值.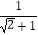 +
+ 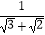 +
+ 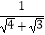 +…+
+…+ 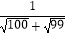
(4)拓展提高,求下列式子的值.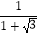 +
+ 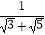 +
+ 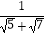 +…+
+…+ 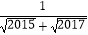 .
.
相关试题

