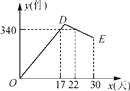
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
参考答案:
【答案】(1)330;660 (2)答案见解析(3) 日销售利润不低于640元的天数共有11天,试销售期间,日销售最大利润是720元.
【解析】
(1)340﹣(24﹣22)×5=330(件),
330×(8﹣6)=660(元).
(2)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
根据题意得:线段DE所表示的y与x之间的函数关系式为y=340﹣5(x﹣22)=﹣5x+450.
联立两线段所表示的函数关系式成方程组,
得![]() ,解得
,解得![]() ,
,
∴交点D的坐标为(18,360),
∴y与x之间的函数关系式为y=![]() .
.
(3)当0≤x≤18时,根据题意得:(8﹣6)×20x≥640,
解得:x≥16;
当18<x≤30时,根据题意得:(8﹣6)×(﹣5x+450)≥640,
解得:x≤26.
∴16≤x≤26.
26﹣16+1=11(天),
∴日销售利润不低于640元的天数共有11天.
∵点D的坐标为(18,360),
∴日最大销售量为360件,
360×2=720(元),
∴试销售期间,日销售最大利润是720元.
-
科目: 来源: 题型:
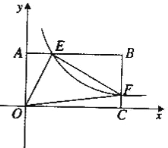
查看答案和解析>>【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数
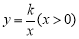 的图象与边BC交于点F。
的图象与边BC交于点F。【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求
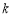 的值:
的值:【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:已知在纸面上有一数轴(如图所示),

(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②
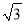 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的材料,再解答后面的各题:
现代社会对保密要求越来越高,密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q,W,E,……,N,M这26个字母依次对应1,2,3,……,25,26这26个自然数(见下表).
Q
W
E
R
T
Y
U
I
O
P
A
S
D
1
2
3
4
5
6
7
8
9
10
11
12
13
F
G
H
J
K
L
Z
X
C
V
B
N
M
14
15
16
17
18
19
20
21
22
23
24
25
26
给出一个变换公式:

将明文转成密文,如:
 ,即R变为L;
,即R变为L;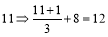 ,即A变为S.
,即A变为S.将密文转换成明文,如:
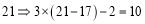 ,即X变为P;13
,即X变为P;13 3×(13-8)-1=14,即D变为F.
3×(13-8)-1=14,即D变为F.(1)按上述方法将明文NET译为密文.
(2)若按上方法将明文译成的密文为DWN,请找出它的明文.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线AB:y
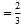 x+4交x轴于点A,交y轴于点B.直线CD:y
x+4交x轴于点A,交y轴于点B.直线CD:y x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E, F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC=
 ,求⊙O的半径.
,求⊙O的半径.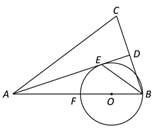
相关试题

