【题目】操作探究:已知在纸面上有一数轴(如图所示),
![]()
(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②![]() 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
参考答案:
【答案】(1) 2; (2)①-3 ; ②![]() ;③A: -3.5,B: 5.5 ;(3)a=2或a=-2
;③A: -3.5,B: 5.5 ;(3)a=2或a=-2
【解析】
(1)根据折叠的性质可直接得出答案;
(2)由-1表示的点与3表示的点重合可以得出对称点为1表示的点,则①表示5的点与对称点的距离为4,与在左侧距对称点距离为4的点重合,从而得出点表示的数;②表示![]() 的点到对称点距离为
的点到对称点距离为![]() -1,与在左侧距对称点距离为
-1,与在左侧距对称点距离为![]() -1的点重合,从而得出点表示的数;③由题意可得A、B两点距离对称点的距离为4.5,之后据此进一步求解即可;
-1的点重合,从而得出点表示的数;③由题意可得A、B两点距离对称点的距离为4.5,之后据此进一步求解即可;
(3)分A向左运动或向右运动两种情况分类讨论求解即可.
(1)∵折叠纸面,使表示的点1与-1重合,
∴对称点为原点,∴-2表示的点与2表示的点重合,
所以答案为2;
(2)∵-1表示的点与3表示的点重合,
∴对称点为1表示的点,
∴①表示5的点与对称点的距离为4,∴与在左侧距对称点距离为4的点重合,
∴此时该点表示的数为-3;
②∵表示![]() 的点到对称点距离为
的点到对称点距离为![]() -1,∴与在左侧距对称点距离为
-1,∴与在左侧距对称点距离为![]() -1的点重合,
-1的点重合,
∴此时该点表示的数为2-![]() ;
;
③∵A、B两点之间距离为9,
∴A、B两点距离对称点的距离为4.5,
∵对称点是1表示的点,
∴A表示的数为:-3.5,B表示的数为:5.5;
(3)①A往左移4个单位:![]() ,a=2;
,a=2;
②A往右移4个单位:![]() ,a=-2.
,a=-2.
综上所述,a的值为2或-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
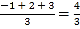 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
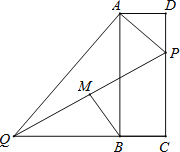
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围.
-
科目: 来源: 题型:
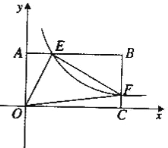
查看答案和解析>>【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数
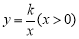 的图象与边BC交于点F。
的图象与边BC交于点F。【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求
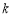 的值:
的值:【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的材料,再解答后面的各题:
现代社会对保密要求越来越高,密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q,W,E,……,N,M这26个字母依次对应1,2,3,……,25,26这26个自然数(见下表).
Q
W
E
R
T
Y
U
I
O
P
A
S
D
1
2
3
4
5
6
7
8
9
10
11
12
13
F
G
H
J
K
L
Z
X
C
V
B
N
M
14
15
16
17
18
19
20
21
22
23
24
25
26
给出一个变换公式:

将明文转成密文,如:
 ,即R变为L;
,即R变为L;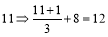 ,即A变为S.
,即A变为S.将密文转换成明文,如:
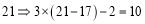 ,即X变为P;13
,即X变为P;13 3×(13-8)-1=14,即D变为F.
3×(13-8)-1=14,即D变为F.(1)按上述方法将明文NET译为密文.
(2)若按上方法将明文译成的密文为DWN,请找出它的明文.
-
科目: 来源: 题型:
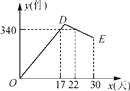
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线AB:y
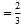 x+4交x轴于点A,交y轴于点B.直线CD:y
x+4交x轴于点A,交y轴于点B.直线CD:y x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.

相关试题

