【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
参考答案:
【答案】(1)-4 ,6-6t ;(2)①点P运动5秒时;②点P运动1或9秒时.
【解析】
(1)由已知得OA=6,则OB=AB-OA=4,因为点B在原点左边,从而写出数轴上点B所表示的数;动点P从点A出发,运动时间为t(t>0)秒,所以运动的单位长度为6t,因为沿数轴向左匀速运动,所以点P所表示的数是6-6t;
(2)①点P运动t秒时追上点Q,由于点P要多运动10个单位才能追上点Q,则6t=10+4t,然后解方程得到t=5;
②分两种情况:当点P运动a秒时,不超过Q,则10+4t-6t=8;超过Q,则10+4t+8=6t;由此求得答案解即可.
解:(1)-4 ,6-6t ;
(2)①根据题意,得6t=10+4t,解得t=5.
答:当点P运动5秒时,点P与点Q相遇.
②当点P在点Q右边时,10+4t-6t=8,解得t=1;
当点P在点Q左边时,10+4t+8=6t,解得t=9.
答:当点P运动1或9秒时,点P与点Q间的距离为8个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓄水池的排水管道每小时排水8
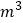 ,6 h可将满池水全部排空.
,6 h可将满池水全部排空.(1)蓄水池的容积是多少?
(2)如果增加排水管道,使 每小时的排水量达到Q(
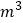 ),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.
),将满池水排空所需时间为t(h),求Q与t之间的函数关系式.(3)如果准备在5h内将满池水排空,那第每小时排水量到少为多少?
(4)已知排水管的最大排水量为每小时12
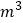 ,那么最少多长时间可将满池水全部排空?
,那么最少多长时间可将满池水全部排空? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以
 cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;

(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
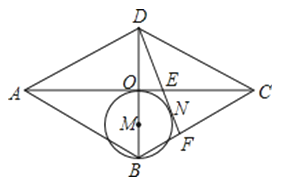
A.3
B.4
C.4.8
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题
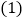 比较大小:
比较大小: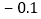 ________
________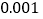 ;
;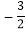 ________
________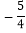 (用“
(用“ 、
、 或
或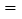 ”填空)
”填空)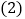 画出数轴,在数轴上表示下列各数,并用“
画出数轴,在数轴上表示下列各数,并用“ ”连接:
”连接: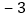 ,
,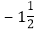 ,
,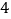 ,
,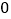 ,
,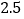
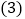 将
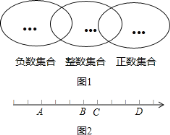
将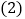 有理数填入图
有理数填入图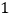 中它所属于的集合的圈内.
中它所属于的集合的圈内. 已知如图
已知如图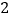 :数轴上
:数轴上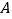 、
、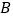 、
、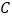 、
、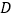 四点对应的有理数分别是整数
四点对应的有理数分别是整数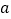 、
、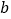 、
、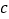 、
、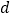 ,且有
,且有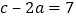 ,则原点应是________.
,则原点应是________.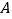 .
.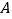 点
点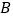 .
.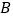 点
点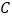 .
.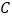 点
点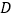 .
.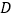 点.
点.
相关试题

