【题目】已知Rt△ABC中,∠C=90°,AC=6,BC=8,点O和M分别为Rt△ABC的外心和内心,线段OM的长为
参考答案:
【答案】![]()
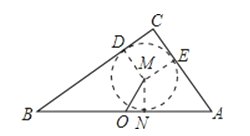
【解析】解:如图,作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.
在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=![]() =10.
=10.
∵点O为△ABC的外心,
∴AO为外接圆半径,AO=![]() AB=5.
AB=5.
设⊙M的半径为r,则MD=ME=r,
又∵∠MDC=∠MEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6﹣r,BD=BN=8﹣r,
∵AB=10,
∴8﹣r+6﹣r=10,
解得r=2,
∴MN=r=2,AN=6﹣r=4.
在Rt△OIN中,∵∠MNO=90°,ON=AO﹣AN=5﹣4=1,
∴OM=![]() =
=![]() .
.
故答案是:![]() .
. 
【考点精析】解答此题的关键在于理解三角形的内切圆与内心的相关知识,掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长a=3,b=4,c=5,则它的内切圆半径是
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,为减少空气污染,北京市一些农村地区实施了煤改气工程,某燃气公司要从燃气站点A向B,C两村铺设天然气管道,经测量得知燃气站点A到B村距离约3千米,到 C村距离约4千米,B,C两村间距离约5千米.下面是施工部门设计的三种铺设管道方案示意图.请你通过计算说明在不考虑其它因素的情况下,下面哪个方案所用管道最短.
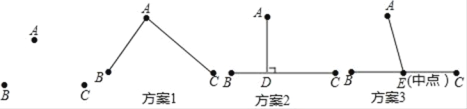
-
科目: 来源: 题型:
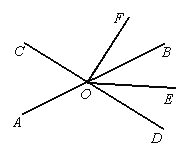
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠AOD=120°,FO⊥OD,OE平分∠BOD.
(1)求∠EOF的度数;
(2)试说明OB平分∠EOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个,这两种玻璃保温杯的进价、标价如表所示:
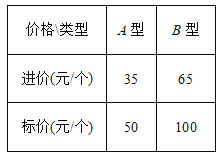
(1)这两种玻璃保温杯各购进多少个?
(2)若A型玻璃保温杯按标价的9折出售,B型玻璃保温杯按标价的8.5折出售,且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏,不能进行销售,请问这批玻璃保温杯全部售出后,该家居专营店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.
(1)求OC的长;
(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;
(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.

相关试题

