【题目】解下列方程(组)
(1)3x=1+2(x﹣2)
(2)![]()
(3)![]()
(4)![]() .
.
参考答案:
【答案】
(1)解:3x=1+2x﹣4,
3x﹣2x=1﹣4,
所以x=﹣3;
(2)解:3(x﹣1)﹣2(2x+1)=6,
3x﹣3﹣4x﹣2=6,
﹣x=11,
所以x=﹣11;
(3)解: ![]() ,
,
由①×2+②得7x=7,
解得x=1,
把x=1代入①得2+y=1,解得y=﹣1,
所以方程组的解为 ![]() ;
;
(4)解: ![]() ,
,
由①得a=2b+4③,
把③代入②得2(2b+4)+b+2=0,
解得b=﹣2,
把b=﹣2代入③得a=0,
所以方程组的解为 ![]()
【解析】(1)先去括号、移项,然后合并即可;(2)先去分母,再去括号,然后移项、合并得到﹣x=11,再把x的系数化为1即可;(3)利用加减消元法解方程组;(4)利用代入消元法解方程组.
【考点精析】关于本题考查的解一元一次方程的步骤和解二元一次方程组,需要了解先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;二元一次方程组:①代入消元法;②加减消元法才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|+
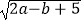 =0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D. 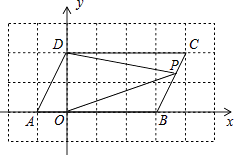
(1)请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D,连接AC,BD,CD.
(2)点E在坐标轴上,且S△BCE=S四边形ABDC , 求满足条件的点E的坐标.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合)证明: 是个常数.
是个常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D.
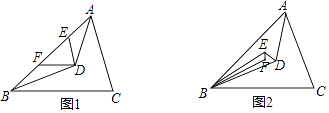
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度? -
科目: 来源: 题型:
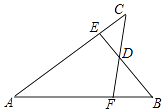
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A.①
B.②
C.①和②
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】去年冬季的某一天,学校一室内温度是8℃,室外温度是﹣2℃,则室内外温度相差℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x﹣4)=2x﹣8.
-
科目: 来源: 题型:
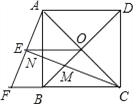
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=
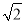 ,求正方形ABCD的边长;
,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.
相关试题

