【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D. 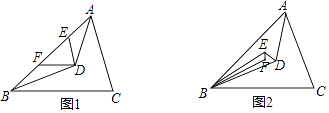
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ ![]() )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度?
参考答案:
【答案】
(1)解:∵∠EDF=80°,
∴∠DEF+∠EDF=180°﹣80°=100°,
∵DE∥AC,
∴∠BED=∠BAC,
同理得:∠EFD=∠ABC,
∴∠ABC+∠BAC=∠DEF+∠EDF=100°,
∴∠C=80°
故答案为:80°;
②∵∠EDF=x°,
∴∠DEF+∠EFD=180°﹣x°,
∵DE∥AC,
∴∠BED=∠BAC,
∵AD平分∠BAC,
∴∠BAC=2∠BAD,
∴∠DEF=2∠BAD,
同理得:∠EFD=2∠ABD,
∴∠BAD+∠ABD= ![]() ,
,
∴∠ADB=180°﹣∠ABD﹣∠BAD=180°﹣ ![]() =90°+
=90°+ ![]() =(90+
=(90+ ![]() )°
)°
(2)解:∵DE平分∠ADB,
∴∠BDE= ![]() ∠ADB=45°+
∠ADB=45°+ ![]() ,
,
∵∠BED+∠DBE=180°﹣∠BDE,
∵EF,BF分别平分∠BED和∠EBD,
∴ ![]() ∠BED+
∠BED+ ![]() ∠DBE=90°﹣
∠DBE=90°﹣ ![]() ∠BDE,
∠BDE,
即∠BEF+∠EBF=90°﹣ ![]() ∠BDE,
∠BDE,
∴∠BFE=180°﹣(∠BEF+∠EBF),
=180°﹣(90°﹣ ![]() ∠BDE),
∠BDE),
=90°+ ![]() ∠BDE,
∠BDE,
=90°+ ![]() (45°+
(45°+ ![]() ),
),
=90°+22°+ ![]() +
+ ![]() ,
,
=112°+ ![]() ,
,
∵∠BFE的度数是整数,
当x=4时,∠BFE=113°.
答:∠BFE至少是113度
【解析】(1)①先根据三角形的内角和求得:∠DEF+∠EDF=100°,再由平行线的性质得:∠BED=∠BAC,∠EFD=∠ABC,所以∠C=180°﹣100°=80°;②同理先求出∠DEF+∠EFD=180°﹣x°,由平行线的性质和角平分线的定义得:∠DEF=2∠BAD,同理得:∠EFD=2∠ABD,则∠BAD+∠ABD= ![]() ,再由三角形内角和可求得结论;(2)依据②的结论得:∠ADB=(90+
,再由三角形内角和可求得结论;(2)依据②的结论得:∠ADB=(90+ ![]() )°,则∠BDE=
)°,则∠BDE= ![]() ∠ADB=45°+
∠ADB=45°+ ![]() ,由三角形的内角和定理得:∠BED+∠DBE=180°﹣∠BDE,再由角平分线定义得:
,由三角形的内角和定理得:∠BED+∠DBE=180°﹣∠BDE,再由角平分线定义得: ![]() ∠BED+
∠BED+ ![]() ∠DBE=90°﹣
∠DBE=90°﹣ ![]() ∠BDE,代入∠BFE=180°﹣(∠BEF+∠EBF),可得结论.
∠BDE,代入∠BFE=180°﹣(∠BEF+∠EBF),可得结论.
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】制造一种产品,原来每件成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低的百分率是( )
A.8.5%
B.9%
C.9.5%
D.10% -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
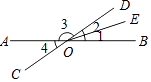
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|+
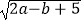 =0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D. 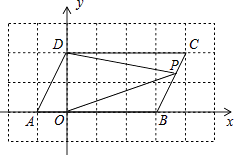
(1)请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D,连接AC,BD,CD.
(2)点E在坐标轴上,且S△BCE=S四边形ABDC , 求满足条件的点E的坐标.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合)证明: 是个常数.
是个常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
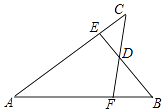
A.①
B.②
C.①和②
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组)
(1)3x=1+2(x﹣2)
(2)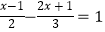
(3)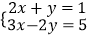
(4)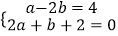 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】去年冬季的某一天,学校一室内温度是8℃,室外温度是﹣2℃,则室内外温度相差℃.
相关试题

