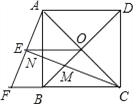
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
参考答案:
【答案】(1)1(2)CN=![]() CM
CM
【解析】试题分析:(1)利用正方形的性质和勾股定理计算即可;
(2)先判断出EO为△AFC的中位线,再由EO∥BC得出![]() ,进而利用直角三角形得出CM=
,进而利用直角三角形得出CM=![]() EM,再判断出△CBN∽△COM得出比例式,进而得出CN=
EM,再判断出△CBN∽△COM得出比例式,进而得出CN=![]() CM,即可得出结论.
CM,即可得出结论.
试题解析:(1)∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD=![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)CN=2CM
理由:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC
∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,AE=FE
∴EO为△AFC的中位线
∴EO∥BC
∴![]()
∴在Rt△AEN中,OA=OC
∴EO=OC=![]() AC,
AC, ![]()
∴CM=![]() EM
EM
∵AF平分∠ACF,
∴∠OCM=∠BCN,
∵∠NBC=∠COM=90°,
∴△CBN∽△COM,
∴![]() ,
,
∴CN=![]() CM.
CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组)
(1)3x=1+2(x﹣2)
(2)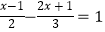
(3)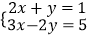
(4)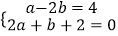 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】去年冬季的某一天,学校一室内温度是8℃,室外温度是﹣2℃,则室内外温度相差℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x﹣4)=2x﹣8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+m的图象与反比例函数y=
 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤
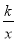 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程x2-ax+a-1=0有两个相等的实数根,那么a的值等于______
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:3(x+2)>﹣1﹣2(x﹣1),并把解集在数轴上表示出来.
相关试题

