【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( ) 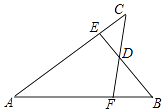
A.①
B.②
C.①和②
D.①②③
参考答案:
【答案】D
【解析】解:如图,连接AD; 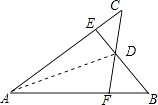
在△ABE与△ACF中,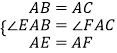 ,
,
∴△ABE≌△ACF(SAS);
∴∠B=∠C;
∵AB=AC,AE=AF,
∴BF=CE;
在△CDE与△BDF中,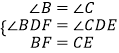 ,
,
∴△CDE≌△BDF(AAS),
∴DC=DB;
在△ADC与△ADB中,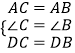 ,
,
∴△ADC≌△ADB(SAS),
∴∠CAD=∠BAD;
综上所述,①②③均正确,
故选D
如图,证明△ABE≌△ACF,得到∠B=∠C;证明△CDE≌△BDF;证明△ADC≌△ADB,得到∠CAD=∠BAD;即可解决问题.
-
科目: 来源: 题型:
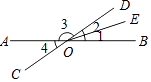
查看答案和解析>>【题目】如图,AB、CD交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|+
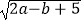 =0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D. 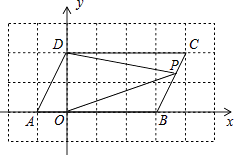
(1)请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D,连接AC,BD,CD.
(2)点E在坐标轴上,且S△BCE=S四边形ABDC , 求满足条件的点E的坐标.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合)证明: 是个常数.
是个常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,BD分别平分∠CAB和∠CBA,相交于点D.
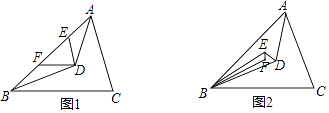
(1)如图1,过点D作DE∥AC,DF∥BC分别交AB于点E、F. ①若∠EDF=80°,则∠C为多少?
②若∠EDF=x°,证明:∠ADB=(90+ )°.
)°.
(2)如图2,若DE,BE分别平分∠ADB和∠ABD,且EF,BF分别平分∠BED和∠EBD,若∠BFE的度数是整数,求∠BFE至少是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组)
(1)3x=1+2(x﹣2)
(2)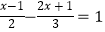
(3)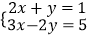
(4)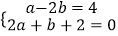 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】去年冬季的某一天,学校一室内温度是8℃,室外温度是﹣2℃,则室内外温度相差℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x﹣4)=2x﹣8.
相关试题

