【题目】某公司计划十月份组织员工到外地旅游,人数在10~30人之间.甲、乙两个旅行社的服务质量相同,且价格都是每人500元.甲旅行社表示可先免去两位游客的旅游费用,其余人九折优惠,乙旅行社表示给予每位游客八折优惠.
(1)写出甲乙两个旅行社收费y与人数x之间的函数关系式.
(2)如果你是这次出游的组织者,当去多少人时两家旅行社的总费用相同.
(3)当去17人时,选哪家旅行社更优惠?请说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)18人;(3)应选择甲旅行社.
;(2)18人;(3)应选择甲旅行社.
【解析】
(1)对甲旅社,根据等量关系“所需费用=报价×(人数-2)×0.9”列出函数关系式;
对乙旅社,根据等量关系“所需费用=报价×0.8×人数”列出函数关系式;
(2)由两家费用相同可得方程500x×0.8=500×(x-2)×0.9,解出即可;
(3)计算出甲乙两旅社各需要的费用,选择优惠的旅行社.
解:(1)由题意得,
甲旅行社费用y与人数x之间的函数表达式:y=500×(x-2)×0.9=450x-900;
乙旅行社费用y与人数x之间的函数表达式:y=500x×0.8=400x,
故答案为:![]() ,
,![]() ;
;
(2)设当人数是x人时,两家旅行社的总费用相同,由题意得:
500x×0.8=500×(x-2)×0.9
400x=450x-900
50x=900
x=18
答:当人数是18人时,两个旅行社旅游费用一样多;
(3)当x=17时,
甲旅行社费用:450×17-900=6750元;
乙旅行社费用:400×17=6800元;
6750<6800,
甲旅行社费用少些;
答:当去17人时,选甲旅行社更优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差S(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中,正确的是 ______(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知 三角形ABC各顶点在格点上
(1)直接写出三角形ABC的三个顶点的坐标
A B C ;
(2)画出三角形ABC关于y轴对称的三角形A′B′C′.
(3)求三角形ABC的面积;
(4)直接与出A′C′与y轴交点的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某地长途汽车站规定前来乘车的旅客可以免费随身携带一定质量的行李,如果行李质量超过规定,则应交纳行李费,行李费用y(元)与行李质量x(千克)之间的关系可以用如图所示的图象表示,请观察图象回答下列问题:

(1)旅客最多能免费携带多少千克的行李?
(2)求行李费用y(元)与行李质量x(千克)之间的函数关系式;
(3)一位旅客随身携带了60千克的行李,他应交纳行李费多少元?
(4)另一位旅客交纳了120元行李费,他携带的行李重多少千克?
-
科目: 来源: 题型:
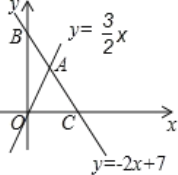
查看答案和解析>>【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=
 x相交于点A.
x相交于点A.(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=
 DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

相关试题

