【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

参考答案:
【答案】(1)见解析(2)10
【解析】
(1)利用正方形的性质,可得∠A=∠D,根据已知条件可知![]() ,根据两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;(2)根据平行线分线段成比例定理,可得CG的长,即可求出BG的长.
,根据两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;(2)根据平行线分线段成比例定理,可得CG的长,即可求出BG的长.
(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC, ∠A=∠D=90°,
∵AE=ED,
∴![]() ,
,
又∵DF=![]() DC,∴
DC,∴![]()
∴![]()
∴△ABE∽△DEF;
(2)解:∵四边形ABCD为正方形,
ED∥BG,
∴![]()
又∵DF=![]() DC,正方形的边长为4,
DC,正方形的边长为4,
∴ED=2,CG=6,
BG=BC+CG=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划十月份组织员工到外地旅游,人数在10~30人之间.甲、乙两个旅行社的服务质量相同,且价格都是每人500元.甲旅行社表示可先免去两位游客的旅游费用,其余人九折优惠,乙旅行社表示给予每位游客八折优惠.
(1)写出甲乙两个旅行社收费y与人数x之间的函数关系式.
(2)如果你是这次出游的组织者,当去多少人时两家旅行社的总费用相同.
(3)当去17人时,选哪家旅行社更优惠?请说明理由.
-
科目: 来源: 题型:
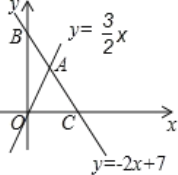
查看答案和解析>>【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=
 x相交于点A.
x相交于点A.(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+2的图象与反比例函数y=﹣
 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.(1)求A、B两点的坐标;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx+n与反比例函数y=
 其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

