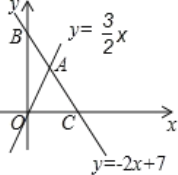
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)A点坐标是(2,3);(2)![]() =
=![]() ;(3)P点坐标是(0,
;(3)P点坐标是(0, ![]() );(4)点Q是坐标是(
);(4)点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
解析
联立方程,解方程即可求得;
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0),由(1)得A点坐标,可得
,0),由(1)得A点坐标,可得![]() 的值;
的值;
(3)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
(4)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据
![]() =
=![]() -
-![]() 列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据
列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据![]() =
=![]() -
- ![]() 列出关于y的方程解方程求得即可.
列出关于y的方程解方程求得即可.
解(1)解方程组: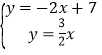 得:
得:![]() ,
,
![]() A点坐标是(2,3);
A点坐标是(2,3);
(2)![]() C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0)
,0)
![]()
![]() =
=![]() =
=![]()
(3)设P点坐标是(0,y ),
![]() △OAP是以OA为底边的等腰三角形,
△OAP是以OA为底边的等腰三角形,
![]() OP=PA,
OP=PA,
![]()
![]() ,
,
解得y=![]() ,
,
![]() P点坐标是(0,
P点坐标是(0, ![]() ),
),
故答案为(0, ![]() );
);
(4)存在;
由直线y=-2x+7可知B(0,7),C(![]() ,0),
,0),
![]()
![]() =
=![]() =
=![]() <6,
<6,
![]() =
=![]() =7>6,
=7>6,
![]() Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图1, 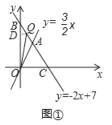
则QD=x,![]()
![]() =
=![]() -
-![]() =7-6=1,
=7-6=1,
![]()
![]() OB
OB![]() QD=1,即:
QD=1,即: ![]()
![]() 7x=1,
7x=1,
![]() x=
x=![]() ,
,
把x=![]() 代入y=-2x+7,得y=
代入y=-2x+7,得y=![]() ,
,
![]() Q的坐标是(
Q的坐标是(![]() ,
,![]() ),
),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图2
则QD=-y,
![]()
![]() =
=![]() -
- ![]() =6-
=6-![]() =
=![]() ,
,
![]()
![]() OC
OC![]() QD=
QD=![]() ,即:
,即:![]() ,
,
![]() y=-
y=-![]() ,
,
把y=-![]() 代入y=-2x+7,解得x=
代入y=-2x+7,解得x=![]()
![]() Q的坐标是(
Q的坐标是(![]() ,-
,-![]() ),
),
综上所述:点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).

(1)分别求直线l1和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D左方时,写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
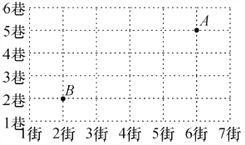
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:
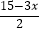 ≥7﹣x,并把它的解集在数轴上表示出来.
≥7﹣x,并把它的解集在数轴上表示出来. 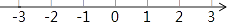
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2
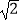 ﹣π)0﹣4cos60°+|
﹣π)0﹣4cos60°+| 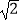 ﹣2|﹣
﹣2|﹣ 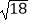 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数 y1=kx+b 与 y2=x+a 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当 x=3 时,y1=y2;④不等式 kx+b>x+a 的解集是 x<3,其中正确的结论有_______.(只填序号)

-
科目: 来源: 题型:
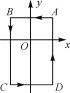
查看答案和解析>>【题目】如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是________.
相关试题

