搜索
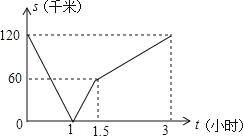
【题目】一辆货车从A地开往B地，一辆小汽车从B地开往A地．同时出发，都匀速行驶，各自到达终点后停止．设货车、小汽车之间的距离为s（千米），货车行驶的时间为t（小时），S与t之间的函数关系如图所示．下列说法中正确的有（ ）
①A、B两地相距60千米；
②出发1小时，货车与小汽车相遇；
③小汽车的速度是货车速度的2倍；
④出发1.5小时，小汽车比货车多行驶了60千米．
A．1个 B．2个 C．3个 D．4个
参考答案：
【答案】C．
【解析】
试题分析：（1）由图象可知，当t=0时，即货车、汽车分别在A、B两地，s=120，
所以A、B两地相距120千米，故①错误；
（2）当t=1时，s=0，表示出发1小时，货车与小汽车相遇，故②正确；
（3）由（3）知小汽车的速度为：120÷1.5=80（千米/小时），货车的速度为40（千米/小时），
∴小汽车的速度是货车速度的2倍，故③正确；
（4）根据图象知，汽车行驶1.5小时达到终点A地，货车行驶3小时到达终点B地，
故货车的速度为：120÷3=40（千米/小时），
出发1.5小时货车行驶的路程为：1.5×40=60（千米），
小汽车行驶1.5小时达到终点A地，即小汽车1.5小时行驶路程为120千米，
故出发1.5小时，小汽车比货车多行驶了60千米，∵故④正确．
∴正确的有②③④三个．
故选：C
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；
（2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由；
（3）点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）给出下列结论： ①
的值不变，② 
的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c经过A（﹣3，0），B（1，0），C（0，3）三点，其顶点为D，对称轴是直线l，l与x轴交于点H．
（1）求该抛物线的解析式；
（2）若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值；
（3）如图（2），若E是线段AD上的一个动点（ E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．
①求S与m的函数关系式；
②S是否存在最大值？若存在，求出最大值及此时点E的坐标； 若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的对角线交于点O ， 以AD为边向外作Rt△ADE ， ∠AED＝90°，连接OE ， DE＝6，OE＝
，则另一直角边AE的长为（ ）.
A.
B.2
C.8
D.10 -
科目： 来源： 题型：
查看答案和解析>>【题目】Rt△ABC中，∠C=90°，∠A=35°30′，则∠B=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B ， 则这个一次函数的解析式是（ ）.
A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为
相关试题
