【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是![]() ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的.
参考答案:
【答案】(1)该网店甲种羽毛球每筒的售价为60元,乙种羽毛球每筒的售价为45元;(2)甲种羽毛球是按原售价打9折销售的.
【解析】
(1)设甲种羽毛球每筒的售价为![]() 元,乙种羽毛球每筒的售价为
元,乙种羽毛球每筒的售价为![]() 元,由条件可列方程组,则可求得答案;
元,由条件可列方程组,则可求得答案;
(2)设甲种羽毛球按原价售价打![]() 折,再根据商品利润率
折,再根据商品利润率![]() ,列出方程即可求解
,列出方程即可求解
(1)设甲种羽毛球每筒的售价为![]() 元,乙种羽毛球每筒的售价为
元,乙种羽毛球每筒的售价为![]() 元,
元,
根据题意得:![]() ,解得
,解得![]() .,
.,
答:该网店甲种羽毛球每筒的售价为![]() 元,乙种羽毛球每筒的售价为
元,乙种羽毛球每筒的售价为![]() 元.
元.
(2)设甲种羽毛球按原价售价打![]() 折,
折,
根据题意得:![]() ,
,
解得:
![]() .
.
答:甲种羽毛球按原价打9折.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6
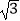 ,AF=4
,AF=4 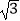 ,则AE的长为 .
,则AE的长为 . 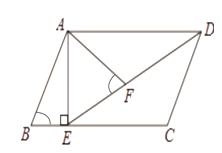
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为
 尺,那么芦苇长用含
尺,那么芦苇长用含 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】小石和小丁利用盒子里的三张卡片做游戏,卡片上分别写有
 ,
, ,
, ,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,
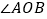 .
.求作:射线
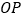 ,使它平分
,使它平分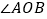 .
.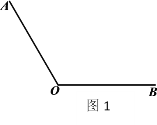
作法:如图2,
①以点
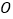 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交 于点
于点 ,交
,交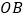 于点
于点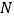 ;
;②分别以点
 ,
,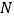 为圆心,以大于
为圆心,以大于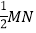 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点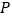 ;
;③作射线
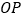 .
.所以射线
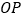 就是所求作的射线.
就是所求作的射线.根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接
 ,
,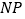 .
.在
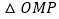 和
和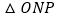 中,
中,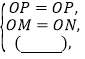
∴
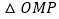 ≌
≌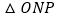 ( )(填推理的依据).
( )(填推理的依据).∴ (全等三角形的 相等).
即射线
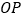 平分
平分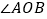 (角平分线定义).
(角平分线定义).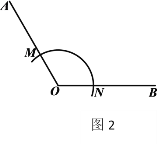
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为进一步发展基础教育,自
 年以来加大了教育经费的投入,
年以来加大了教育经费的投入, 年该地区投入教育经费
年该地区投入教育经费 万元,
万元, 年投入教育经费
年投入教育经费 万元.
万元.(1)求该地区这两年投入教育经费的年平均增长率;
(2)若该地区教育经费的投入还将保持相同的年平均增长率,请预算
 年该地区投入教育经费为 万元.
年该地区投入教育经费为 万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x满足条件
 时,求出方程x2﹣2x﹣4=0的根.
时,求出方程x2﹣2x﹣4=0的根.
相关试题

