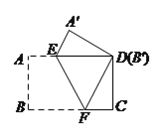
【题目】把一张长方形纸片按如图方式折叠,使顶点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() .若
.若![]() ,
, ![]() .
.
求(![]() )
)![]() 的长.
的长.
(![]() )重叠部分
)重叠部分![]() 的面积.
的面积.
参考答案:
【答案】(1)3.4;(2)5.1
【解析】试题分析:(1)根据折叠的性质知:BF=DF,用DF表示出FC,在Rt△DCF中,利用勾股定理可求得DF的长;
(2)作FH⊥AD于点H,求得FH,由折叠的性质和平行线的性质证得∠EFD=∠DEF,得出DE=DF,进一步利用三角形的面积计算公式即可求解.
试题解析:
解:(1)设DF=x,
由折叠可知BF=DF=x,
∴FC=BC-BF=5-x,
∵四边形ABCD为长方形,
∴DC=AB=3,∠C=90°,AD∥BC,
在Rt△DCF中,∠C=90°,DF2=DC2+FC2
x2=32+(5-x)2
x=3.4,
∴DF=3.4cm;
(2)作FH⊥AD于点H,
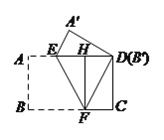
则FH=AB=3,
由折叠可知,
∠EFB=∠EFD,
∵AD∥BC,
∴∠DEF=∠EFB,
∴∠EFD=∠DEF,
∴ED=DF=3.4,
S△DEF=![]() ×DE×FH=
×DE×FH=![]() ×3.4×3=5.1.
×3.4×3=5.1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将7张如图1所示的长为a,宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,求a,b满足的条件.

-
科目: 来源: 题型:
查看答案和解析>>【题目】合并下列多项式中的同类项:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣
 a2b
a2b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为( )

A. 36° B. 45° C. 60° D. 72°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=
 ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:
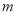
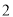
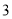
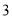
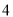
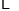
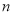
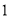
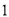
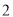
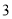
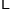
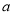
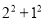
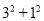
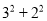
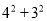
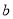
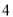
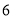
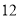
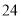
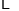
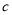
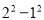
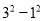
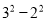
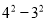
其中
 、
、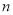 为正整数,且
为正整数,且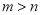 .
.(
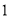 )观察表格,当
)观察表格,当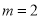 ,
, 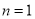 时,此时对应的
时,此时对应的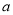 、
、 、
、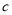 的值能否为直角三角形三边的长?说明你的理由.
的值能否为直角三角形三边的长?说明你的理由.(
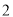 )探究
)探究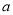 ,
, 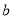 ,
, 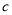 与
与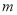 、
、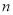 之间的关系并用含
之间的关系并用含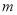 、
、 的代数式表示:
的代数式表示: 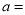 __________,
__________, 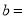 __________,
__________,  __________.
__________.(
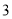 )以
)以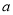 ,
, 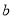 ,
, 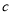 为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=
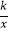 (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 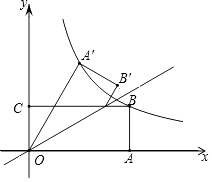
相关试题

